模具t0阶段验证什么(（烧脑计算推导）注塑模具中零件冷却时间的计算方法)

在注塑生产中，塑料件的冷却时间在一定程度上决定了生产的循环时间。在给定的生产条件下，正确计算塑件的冷却时间是设计注塑模冷却系统的关键。影响塑件冷却时间的因素很多，如塑料种类、 熔料温度、塑件开模温度、模具温度等。为了推导注塑件冷却时间的计算公式, 需要进行如下假设：

( 1) 将塑件看成无限大的平板, 忽略从成型塑件侧面进 行的冷却，热流方向沿其厚度方向简化为无内热源 的一维非稳态导热问题；

( 2) 熔料完全依赖模具传 热冷却；

( 3) 塑料的比热容和热传导系数为定值, 不 随温度变化；

( 4) 模具热传导系数为常数, 并假设模 具与塑件始终紧密接触。 在上述假设情况下得到下列数学模型。导热微分方程：

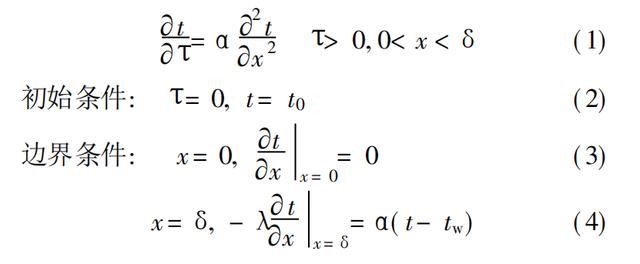
其中 t 为任意时间和空间的温度，℃；T 为冷却时间，s；x为塑件中心距型腔壁的距离， mm；δ为塑件厚度的一半，mm; a为材料的导温系数, mm²/ s; α为材料的换热系数，W/ (m²• ℃) ; λ为导热系数, W/m• ℃; t0 为塑料的注射温度, ℃；tw为型腔壁的温度，℃；tc 为热变形温度, ℃。引入新的变量过余温度 0= t - t w, 则( 1) ~ ( 4) 改写为:

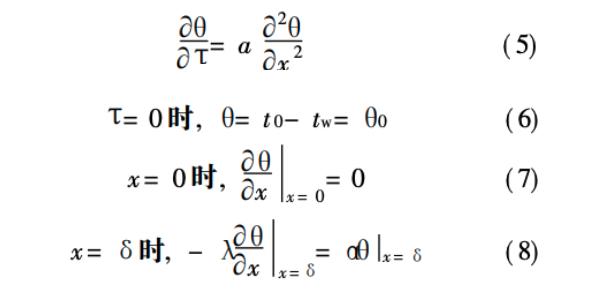
由于解此高阶方程常用数值分析方法，本文采用分离变量法，求解上述微分方程，将偏微分方程式( 5) 的解表示成两个独立的单变量函数的乘积，使偏微分方程转化为两个微分方程式，进行求解。

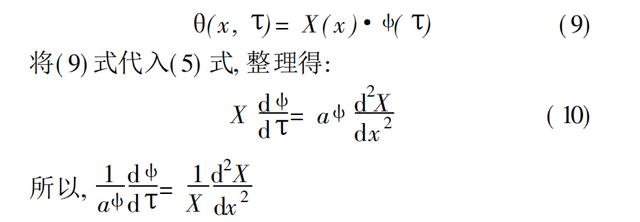
( 10) 式的两端各是一个自变量的函数, 故只有当等式两端各自等于同一个常数时才能成立。令此常数为 m, 则有( 10) 式可得两个常微分方程式:

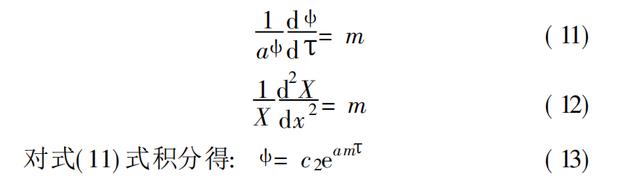
式中：c₁为积分常数。常数m的正负可以从物理意义上加以确定，在塑料平板被冷却的过程中，当冷却时间T→∞时, 过程达到稳态。塑料平板的温度等于模具型腔壁的温度(θ=0) , 此时，(13）式中的m只能为负值。否则, 当T→∞时，Φ→∞，则 0( x , T)→∞，这实际上是不可能的。设 m = -ε², 代入( 11)式、( 12) 式得：

为了确定( 19) 式中的 C₁ 将( 19) 式代入边界条件( 8) 式得：

方程( 22) 式的根见图 1。

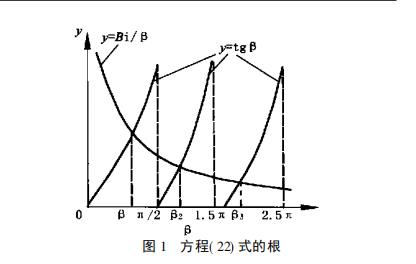
(22) 式中的解是曲线y=tgβ，y=Bi/β的交点，由图可见，有无穷多解，而β=εδ，所以ε也有无

穷多解。由式(19)式知，θ( xT) 也必有无穷多解, 即：

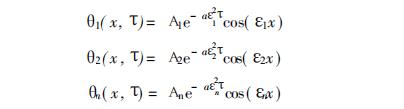
将所有的解线性相加，就得到θ(x,T)的通解：

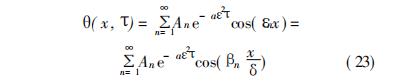
求解（23）式中的未知数An。将边界条件（6）式代入（23）式得：

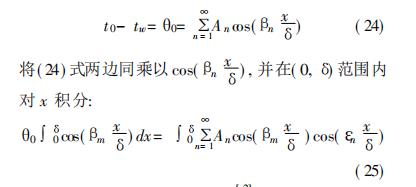
考虑到特征函数的正交性，当m≠n（即βm≠βn）时：

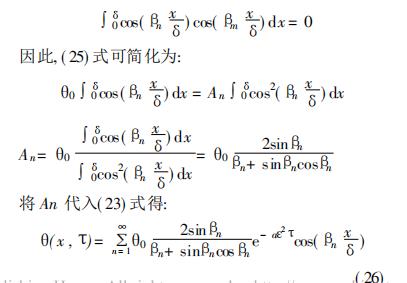
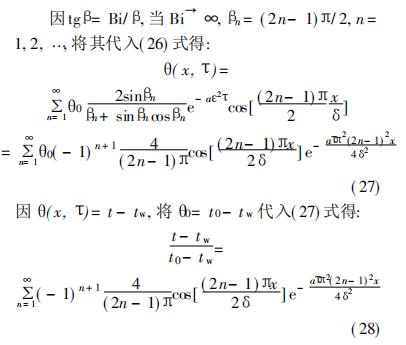
选取不同开模温度点推导出的冷却时间计算公式也不同。图3( a) 为塑件中心温度达到 t c 时的开模，图 3( b) 为距塑件中心1/3δ处达到tc时的开模。

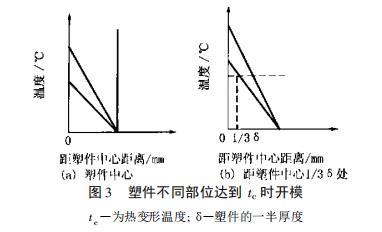
以成型零件最大壁厚中心部分达到开模温度计算冷却时间，选取图3(a)中的c点温度作为开模温度( 热变形温度)tc，即x=0，t=tc，代入(28)式得：

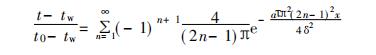
式中: tc 为塑料固化温度，℃。取 n = 1, 两边取对数整理得:

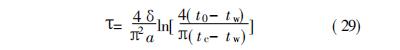
式( 29) 为冷却时间的计算公式，与塑料成型工艺的结论吻合，故推导是正确的。选取c点的温度作为开模温度，这时开模后塑件内外的温度都在固化温度以下，脱模后，塑件不会产生变形，从而保证了质量，但计算出来的时间相对较长。可以根据 实际情况设置某一点的固化温度作为开模温度，代入( 28) 式推导出关系来指导注塑件的生产, 既能保 证塑件的质量, 又能缩短注射成型周期, 提高生产 率。譬如，现取距塑件中心1/3δ处达到的固化温度 作为开模温度, 见图 3( b) , 即 x = 1/ 3δ，t= tc，代入 ( 28) 式得：

取n=1，两边取对数得：

在生产实际中，可用此公式来指导生产。

END

更多模具知识，尽在【奇模智库】，在线模具知识库

公众号：qimozhiku