桥梁钢筋保护层厚度规范要求(公路混凝土桥梁正常使用极限状态可靠度研究综述)

Posted 2023-05-30

篇首语：少年恃险若平地，独倚长剑凌清秋。本文由小常识网(cha138.com)小编为大家整理，主要介绍了桥梁钢筋保护层厚度规范要求(公路混凝土桥梁正常使用极限状态可靠度研究综述)相关的知识，希望对你有一定的参考价值。

桥梁钢筋保护层厚度规范要求(公路混凝土桥梁正常使用极限状态可靠度研究综述)

刘经伟代攀陈军刚涂莹莹许鹏何能

云南省交通规划设计研究院有限公司云南通衢工程检测有限公司重庆市市政设计研究院

摘要：公路混凝土桥梁在服役期内应同时满足安全性与适用性的要求，目前国内外关于桥梁结构可靠度的研究主要集中于承载能力极限状态，正常使用极限状态可靠度研究相对较少。为进一步明确公路混凝土桥梁正常使用极限状态可靠度研究方向并为后续研究以及结构设计、评估及维养等工作提供参考，对现阶段公路混凝土桥梁正常使用极限状态可靠度研究现状进行总结梳理，具体包括正常使用极限状态分析相关规定、目标可靠度指标、失效准则与功能函数、不确定性因素处理方法以及正常使用极限状态可靠度分析方法等。最后，在上述总结梳理的基础上，结合当前研究现状的不足及工程需求，对该领域下一步的研究方向及重点进行分析展望。

关键词：桥梁工程;混凝土桥梁;正常使用极限状态;可靠度;失效准则;

对公路混凝土桥梁在运营阶段的服役性能要求主要体现在安全性与适用性两个方面。安全性要求主要关注结构或构件的极限承载力、稳定性及延性等方面，而适用性主要对应于结构或构件的变形、裂缝宽度、振动等方面的要求。对于与安全性要求相匹配的承载能力极限状态，结构或构件的安全与失效之间的分界线是十分清晰的，例如材料破坏、结构失稳等都是较为清晰的物理现象，截止目前为止，国内外研究人员对承载能力极限状态下的结构或构件可靠度开展了大量研究，且目前各国承载能力极限状态下的结构设计理念、设计方法亦普遍采用了相应的研究成果。对于结构或构件的正常使用极限状态而言，能否达到正常使用要求的分界线是模糊的，很难找到清晰的物理现象与之相对应，正常使用要求是否能够达到的区分，亦在较大程度上依赖于工程经验，故相较之下，关于桥梁结构正常使用极限状态可靠度的研究相对较少，且各国结构设计规范中对结构构件正常使用极限状态设计方法亦存在不同程度的简化处理。

截止目前为止，公路混凝土桥梁运营阶段安全性问题仍是维养工作关注的重中之重，但由于正常使用极限状态下的结构适用性问题直接影响到其能否达到长寿命健康运营的目标，故正常使用极限状态下的结构可靠度研究工作十分必要。已有工程实践表明，某些情况下正常使用极限状态可能对结构起控制作用，与此同时，根据已有的工程灾害统计数据，灾难性的结构失效事件非常少，而正常使用极限状态下的失效事件频频发生，根据一些国家的调查数据，正常使用极限状态下的失效事件是造成结构运营阶段经济损失的主要诱因，例如在美国，由于公路桥梁钢筋锈蚀问题所带来的经济损失约为83亿美元/年，其中大约40亿美元被用于钢混桥面板及上部结构的维护。鉴于此，国际社会明确了对结构进行正常使用极限状态设计及运营阶段维护的必要性。

公路混凝土桥梁正常使用极限状态下的设计与运维等工作需要以大量研究成果为支撑，尽管与承载能力极限状态可靠度研究相比数量较少，但自上世纪80年代中期以来，公路桥梁正常使用极限状态可靠度研究亦经历了一个长期积累的过程，在早期，Ellingwood、赵国藩、贡金鑫、Stewart、Picard等相继对适用性关键指标控制下的正常使用极限状态可靠度展开探索。近20年来，国内外研究人员亦相继在正常使用极限状态目标可靠度指标校准、不同功能函数下正常使用极限状态可靠度分析等方面展开研究。截止目前，公路混凝土桥梁正常使用极限状态可靠度研究所关注的指标主要集中于变形、抗裂度、裂缝宽度、应力水平等。

在此，首先对公路混凝土桥梁正常使用极限状态可靠度相关研究进行总结梳理，以期为该类结构正常使用极限状态设计方法优化、运营阶段适用性评估等工作提供参考，主要综述内容包括:(1)我国规范对正常使用极限状态可靠度分析的相关规定;(2)公路混凝土桥梁正常使用极限状态目标可靠指标;(3)正常使用极限状态失效准则及功能函数建立方法;(4)正常使用极限状态下可靠度分析工作中不确定性因素的处理方法;(5)正常使用极限状态可靠度分析所采用的分析方法。最后，结合当前研究进展及工程需求，对公路混凝土桥梁正常使用极限状态可靠度的进一步研究方向进行展望。

1 正常使用极限状态分析相关规定

正常使用极限状态对应于结构或构件达到正常使用或耐久性某项规定限值的状态。文献[4]中进一步将正常使用极限状态划分为可逆与不可逆两种，所谓不可逆正常使用极限状态指当产生超越正常使用极限状态的作用卸除之后，由该作用产生的超越状态不可恢复。对于结构设计而言，不可逆与可逆正常使用极限状态的区分十分重要，对于不可逆正常使用极限状态应采用标准组合，对于可逆正常使用极限状态应采用准永久组合或频遇组合。此外，可逆与不可逆极限状态的区分不仅要根据构件实际情况确定，应同时考虑该构件与周边构件的联系。对于公路混凝土桥梁正常使用极限状态可靠度分析工作，现行规范中各正常使用指标的计算及控制方法是功能函数建立的依据，在此，依次介绍现行规范对公路混凝土桥梁构件变形、裂缝、应力等关键指标的计算及控制方法。

1.1 变形分析及控制方法

构件刚度的确定是公路混凝土桥梁构件变形分析的基础，同时亦将影响到变形控制下正常使用极限状态功能函数的建立。根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)，钢筋混凝土及预应力混凝土受弯构件的变形可在准确确定构件刚度的基础上，采用结构力学方法予以计算。对于钢筋混凝土受弯构件，当其所承受的弯矩大于开裂弯矩时，构件刚度为:

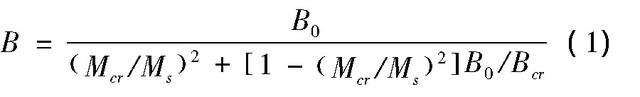
其中，Ms为构件所承受弯矩值，结构设计时为按作用频遇组合计算的弯矩值;Mcr为受弯构件的开裂弯矩，Mcr=γftkW0，γ、ftk、W0分别表示受拉区混凝土塑性影响系数、混凝土轴心抗拉强度标准值以及换算截面受拉边缘弹性抵抗矩;B为开裂构件的等效截面抗弯刚度;B0为受弯构件全截面抗弯刚度，B0=0.95EcI0,Ec、I0分别表示混凝土弹性模量以及全截面换算截面惯性矩;Bcr=EcIcr为开裂截面抗弯刚度，Icr表示开裂构件换算截面惯性矩。若Ms<Mcr，受弯构件刚度为B=B0。

关于钢混开裂构件实际抗弯刚度，Castel等考虑弯曲裂缝之间因受拉区钢混粘结力所导致的混凝土受拉刚化效应，提出了基于宏观有限元思想的开裂构件弯曲变形计算方法，该方法中将相邻弯曲裂缝间的构件处理为一个宏观有限单元，考虑构件开裂及混凝土受拉刚化效应的宏观有限单元平均惯性矩为:

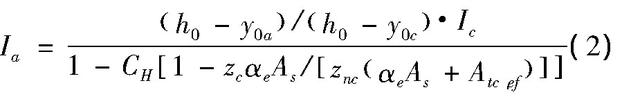
其中，Ia为宏观有限单元平均惯性矩;h0为截面有效高度;y0a为宏观有限单元中性轴平均高度处距离构件上表面的距离;y0c为开裂截面中性轴位置距离构件上表面的距离;Ic为开裂截面抗弯惯性矩;zc、znc分别为开裂截面及未开裂截面内力臂;αe为钢筋与混凝土瞬时弹性模量之比;As、Atc,ef分别表示受拉钢筋截面积及有效混凝土受拉截面积;CH为混凝土均质化系数，该系数取值取决于钢混粘结力传递长度与半个裂缝间距的比值，在实际中，对每一个构件进行均质化系数的计算困难较大，考虑到裂缝间距一般不小于传递长度且不超过两倍的传递长度，故传递长度与半个裂缝间距的比值介于0.5～1.0之间，欧洲混凝土协会将比值建议为0.75并由此得到CH≈0.65625。

此外，受弯构件在服役阶段的变形分析尚应考虑混凝土收缩、徐变等长期效应的影响，具体分析时将短期效应挠度值乘以长期增长系数ηθ，ηθ取值方法为采用C40以下混凝土时为1.60，采用C40～C80混凝土时在1.45～1.35之间插值。在文献[19]的基础上，Castel等进一步考虑钢混粘结界面损伤以及混凝土收缩、徐变等长期效应的影响，对钢混开裂构件的瞬时抗弯刚度进行了研究。

文献[18]并未明确指出钢混及预应力混凝土受弯构件的挠度限值，根据文献[21]的规定，钢混及预应力混凝土受弯构件的长期挠度值，在消除结构自重产生的长期挠度后梁式桥主梁的最大挠度处不应超过计算跨径的1/600，梁式桥主梁悬臂端不应超过悬臂长度的1/300。文献[17]详细讨论了桥梁运营阶段挠度限值的制定方法。

1.2 裂缝分析及控制方法

钢筋混凝土桥梁构件因抗裂能力相对较低通常处于一种带裂缝工作状态，主要裂缝种类包括因弯曲应力产生的横向裂缝、因钢筋锈蚀产物膨胀导致的纵向受力裂缝以及因温度变化导致的网状裂缝等。在裂缝宽度分析计算方面，后两者因影响因素复杂且难以量化尚未形成明确的计算方法。根据文献[18],B类预应力混凝土受弯构件及钢混受弯构件横向裂缝宽度计算方法为:

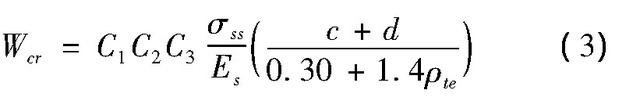
其中，C1为钢筋表面形状系数，对光面钢筋、带肋钢筋及环氧图层钢筋分别取1.40、1.00与1.15;C2=1+0.5Ml/Ms为长期效应影响系数，Ml、Ms分别为按照作用准永久组合及作用频遇组合计算的弯矩值;C3为与构件受力性质有关的系数，对钢混板式受弯构件及其他受弯构件分别取为1.15与1.0;σss为钢筋应力，c为最外排纵向受拉钢筋的混凝土保护层厚度(mm);d为纵向受拉钢筋，采用不同直径的钢筋时，采用换算直径;ρte为纵向受拉钢筋的有效配筋率。

现阶段对公路混凝土桥梁的裂缝控制主要采用防裂与限裂两种途径，防裂主要通过提升截面的开裂弯矩以提升抗裂度，而限裂主要通过控制最大裂缝宽度实现。文献[18]同时给出了不同环境类别急不同构件类型所对应的最大裂缝宽度限值，例如I类-一般环境下钢混构件最大裂缝宽度限值为0.2mm。

1.3 预应力构件应力分析及控制方法

对于A类及B类预应力混凝土构件，正截面及斜截面混凝土应力是其设计及运营阶段正常使用性能保障的重要指标，对于正截面及斜截面混凝土分别控制相应的法向拉应力及主拉应力。正截面混凝土法向拉应力控制方法为:(1)全预应力预制构件σst-0.85σpc≤0，分段浇筑或砂浆接缝的纵向分块构件σst-0.80σpc≤0;(2) A类预应力混凝土构件σst-σpc≤0.7ftk、σlt-σpc≤0;(3) B类预应力混凝土构件在结构自重作用下控制截面受拉边缘不得消压。其中，σst为作用频遇值组合下构件抗裂验算截面边缘混凝土法向拉应力;σlt为在作用准永久组合下构件控制截面边缘混凝土法向拉应力;σpc为有效预加力在构件控制截面边缘产生的混凝土预压应力;ftk为混凝土的抗拉强度标准值。

2 公路桥梁结构正常使用极限状态目标可靠指标

2.1 基准期

公路混凝土桥梁结构以规定的目标可靠指标进行承载能力及正常使用极限状态设计。需要特别指出，目标可靠指标的声明必须与特定的基准期一一对应，比如我国现行公路桥梁承载能力极限状态设计目标可靠度指标对应的基准期为100年。任意基准期所对应目标可靠指标与年目标可靠指标的相互换算关系为:

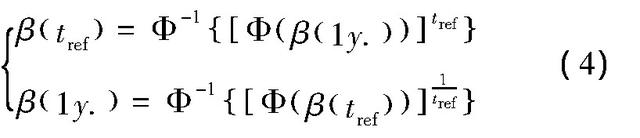
其中，β(tref)为任意基准期tref对应的目标可靠指标;β(1y.)为年目标可靠指标;Φ-1(·)为标准正态分布函数的反函数。

当前国内外规范对正常使用极限状态目标可靠指标的声明多采用两类基准期，即1年与全寿命，例如JCSS在规定正常使用极限状态设计目标可靠指标时基准期为1年，ISO采用全寿命时间尺度给出了目标可靠指标，欧洲规范在规定正常使用极限状态目标可靠指标时同时采用了1年基准期及设计基准期。根据文献[22]对正常使用极限状态设计基准期的建议，桥梁结构一般通车状态下卸载后不会产生永久损坏，设计基准期可按取为1年。故对于运营阶段的桥梁养护及评估工作，正常使用极限状态评估分析基准期可采用1年。

2.2 目标可靠指标

正常使用极限状态设计目标可靠指标的确定多根据相应结构的具体特点及工程经验确定。《公路工程结构可靠度设计统一标准》(GB/T 50283-1999)在制定过程中对我国公路混凝土桥梁裂缝及挠度隐含的可靠度水平进行校准，校准过程中采用设计汽车荷载，结果显示设计基准期所对应的最小目标可靠指标为1.0，根据式(4)，对应的年目标可靠指标为2.92。表1给出了JCSS、ISO以及欧洲规范对不同失效后果、不同基准期所对应的正常使用极限状态设计目标可靠度指标取值。对比可知，我国桥梁结构设计中对正常使用极限状态失效概率的控制水平与欧洲规范十分接近，略低于JCSS建议水平，与ISO所建议的较低水平的目标可靠指标接近。Lenner等在ISO所提供的方法框架之下，建立了一种针对正常使用极限状态目标可靠指标合理性考证的方法。

表1 国际规范中正常使用极限状态目标可靠指标下载原图

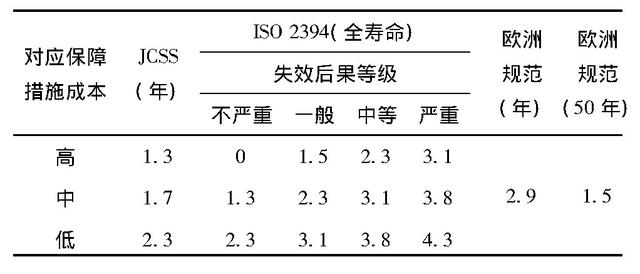
3 正常使用极限状态失效准则及功能函数

能够反映公路桥梁正常使用性能的指标很多，根据正常使用极限状态失效准则定义的不同，可分别建立相应关键指标控制下的正常使用极限状态可靠度分析功能函数。截止目前，被用于定义正常使用极限状态失效准则的关键指标包括构件挠度、抗裂度、裂缝宽度、应力水平、碳化深度等。上述指标的力学分析计算相对复杂且过程中或多或少地引入了相关假定，现有研究在功能函数建立过程中多通过计算模式不确定性随机变量的引入来反应人为认知不定性。

3.1 挠度

采用挠度为控制指标进行正常使用极限状态可靠度分析时，失效准则定义方法为构件最大挠度超越现行规范所规定的允许值，相应的功能函数可建立为:

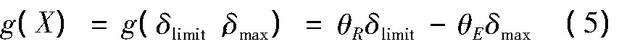
其中，X为基准随机变量向量;δlimit，δmax分别表示容许位移随机变量及特定基准期内最大位移随机变量，亦分别称为广义抗力与广义荷载效应;θR、θE分别表示广义抗力计算模型不确定性系数以及位移效应计算方法不确定性系数。

对于δmax，较短基准期内的变形可靠度分析可不考虑长期效应的影响，而考虑较长基准期时尚应计入混凝土收缩、徐变等长期效应的影响，文献[11]在开展挠度可靠度分析的δmax计算过程中同时考虑了瞬时变形、收缩及徐变等，所得到的δmax为时变随机变量。文献[6]对开裂钢混构件的挠度可靠度进行分析，结果发现由于钢筋锈蚀所导致的结构开裂对钢混梁正常使用性能的影响较变形增大所带来的影响更为显著。

3.2 应力水平

对于全预应力构件及A类预应力构件，控制截面混凝土拉应力是其正常使用性能保障主要关注的指标之一，但截止目前，以混凝土应力为控制指标的可靠度研究开展较少。姚继涛等对受弯混凝土构件混凝土应力控制下的可靠度展开研究，对σck-σpc≤0及σck-σpc≤ftk两种限裂等级的受弯构件所建立的功能函数为:

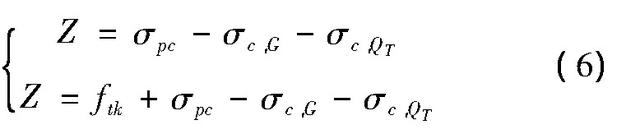
其中，σc,k、σc,G、σc,QT分别表示控制截面混凝土受拉区边缘法向拉应力、由恒载作用产生的混凝土法向拉应力以及由特定基准期最大活载效应产生的混凝土法向拉应力。

3.3 横向抗裂度

横向抗裂度作为关键指标进行可靠度分析时，以不允许出现横向弯曲裂缝作为正常使用极限状态失效准则的定义依据。其功能函数建立方法为控制截面所承受的弯矩水平不应超过截面的开裂弯矩，对应的功能函数为:

其中，[Mf]为控制截面的开裂弯矩，在此作为广义抗力随机变量，在式(7)所示的功能函数中，开裂弯矩计算模式不确定性系数已包含在广义抗力计算过程中，故不再在功能函数中单独作为一个随机变量体现;MT为特定基准期内弯矩效应最大值随机变量。

3.4 横向裂缝宽度

在正常使用极限状态可靠度分析过程中，横向裂缝宽度作为关键指标的使用最为频繁。功能函数建立方法为特定基准期内荷载效应最大值随机变量组合所产生的弯曲裂缝宽度不应超过相应条件下的允许值，根据式(3)所示横向裂缝宽度计算方法，可建立如下形式的功能函数:

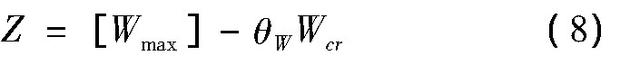
其中，[Wmax)为允许裂缝宽度，作为广义抗力;Wfk为裂缝宽度随机变量;θW为横向裂缝宽度计算方法对应的不确定性系数。结合式(3)，式(8)可进一步变形为:

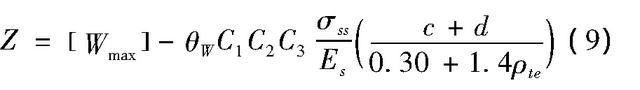
3.5 纵向抗裂度

与横向裂缝不同，纵向裂缝通常是由纵向受拉钢筋锈蚀后锈蚀产物的膨胀所导致，以纵向抗裂度为关键指标进行可靠度分析时，将构件保护层混凝土表面出现锈胀纵向裂缝作为正常使用极限状态。功能函数建立过程中，广义抗力选择为保护层混凝土表面出现锈胀裂缝时刻的钢筋锈胀力，广义荷载效应可选择为钢筋锈胀力，根据赵羽习的研究，保护层混凝土胀裂之前埋置在混凝土中的钢筋锈胀力为:

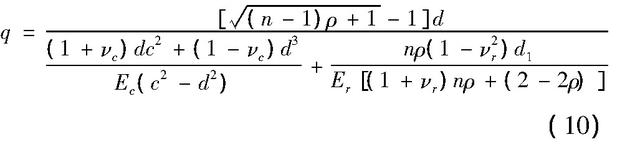
其中，q表示钢筋锈胀力，单位N/mm;ρ表示钢筋锈蚀率;d表示钢筋初始半径(mm);d1表示铁锈自由膨胀后的钢筋半径(mm);νc、c分别表示混凝土泊松比及保护层厚度;Ec、Er分别表示混凝土弹性模量以及铁锈名义弹性模量;νr为铁锈名义泊松比。

混凝土保护层表面胀裂时刻的锈蚀钢筋膨胀力为:

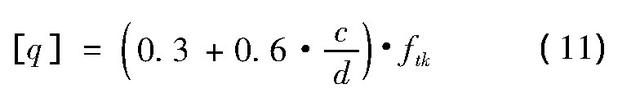
进一步引入计算模式不确定性系数之后的功能函数可建立为:

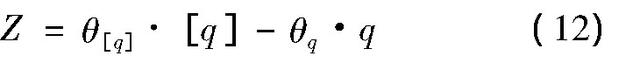
其中，θ[q]、θq分别为广义抗力及广义荷载效应计算模式不确定性系数。

3.6 纵向裂缝宽度

以纵向裂缝宽度为关键指标开展混凝土构件正常使用极限状态下的可靠度分析时，首先需要建立钢筋锈蚀率与纵向裂缝宽度之间的关系，根据王深等的研究，二者之间的关系为:

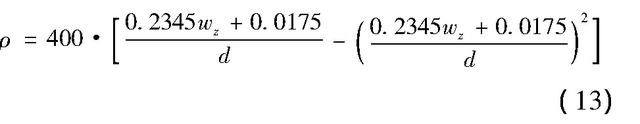
其中，ρ表示钢筋锈蚀率(%)，wz表示纵裂缝宽度(mm)，由式(13):

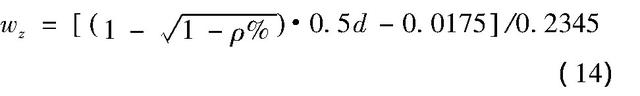
相应的功能函数可建立为:

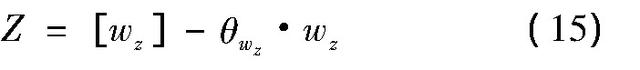
其中，[wz]、θwz分别表示纵向裂缝容许宽度及计算模式不确定性随机变量。

3.7 碳化深度

混凝土保护层碳化是构件内部钢筋脱钝及承载力劣化的主要诱因，以碳化深度为关键指标进行正常使用极限状态可靠度分析时，失效准则为混凝土碳化深度达到钢筋表面，广义抗力与广义荷载效应分别选择为混凝土保护层厚度以及混凝土碳化深度。

混凝土碳化深度预测方法为:

其中，D为t时刻混凝土碳化深度(mm);D0为t0时刻混凝土碳化深度(mm)，λ为混凝土碳化指数。

进一步结合保护层厚度可建立碳化深度控制下的正常使用极限状态可靠度分析功能函数:

其中，θD为碳化深度计算模式不确定性系数。

4 不确定性因素处理方法

由第4节内容可知，在力学分析及现行相关规范方法的基础上，可以在选择关键指标的前提下较为清晰地对正常使用极限状态可靠度分析的功能函数进行定义。但根据所建立的功能函数可知，相比于承载能力极限状态可靠度分析，正常使用极限状态可靠度分析所涉及的随机变量以及认知不确定性因素更为复杂，根据各类不确定性在功能函数中的存在形式，可以总体划分为计算模式不确定性因素、几何参数不确定性因素、材料特性不确定性因素、广义抗力随机性及荷载效应随机性等。以上不确定性因素概率层面的量化处理是开展可靠度分析的基础。

4.1 计算模式不确定性

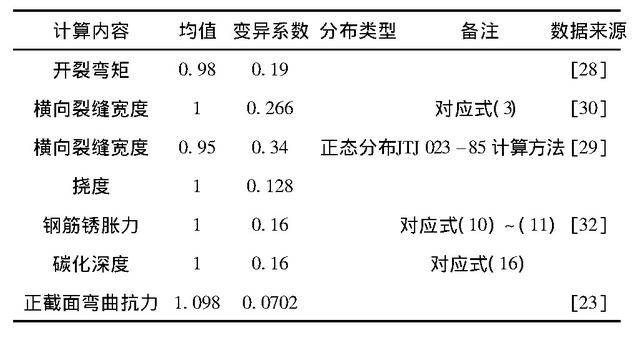
广义抗力及广义荷载效应计算过程中均涉及计算模式不确定性因素的处理。计算模式不确定性系数的分布类型及统计参数确定方法为:通过将根据计算模式计算所得到的结果与按精确模式计算得到的分析结果相比较，经统计分析进行估计，或者借助工程经验进行判断，Qin等采用该方法对裂缝宽度计算方法所对应的计算模式不确定性系数的统计特性进行了分析。对已有研究中各种计算模式不确定性系数的统计特性进行汇总，如表2所示。需要指出，由于早期正常使用极限状态可靠度分析中多采用中心点法展开，所以并未关注计算模式不确定性系数的分布类型，而从近期研究中发现，计算模式不确定性系数的分布类型可认为不拒绝正态分布。

表2 计算模式不确定性系数统计特性下载原图

4.2 几何参数模式不确定性

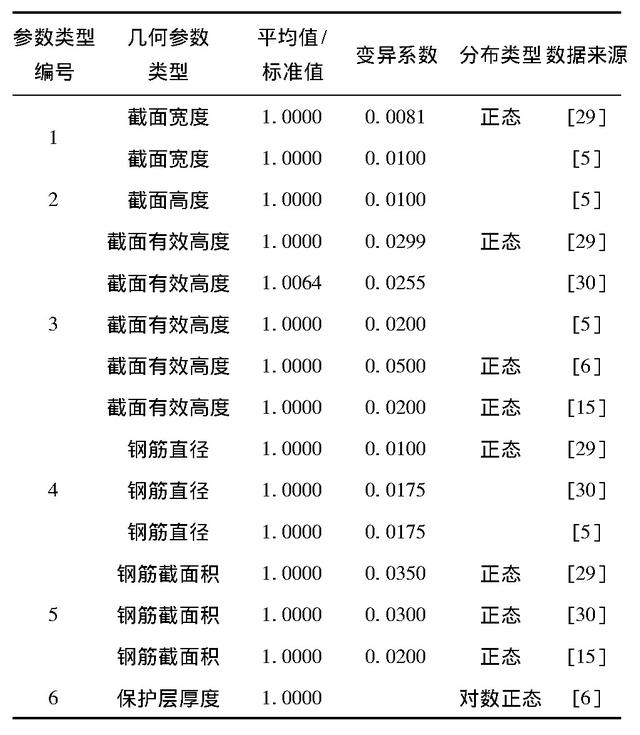
根据文献[23]的建议，当统计数据不充足时，几何参数的概率分布类型可处理为正态分布，统计参数的确定可依据有关标准规定的公差经过分析得到，此外，几何参数标准值根据设计文件的规定值采用。对已有研究中关于几何参数分布类型及统计参数的取用情况进行总结归纳，如表3所示，可见在以往研究中，多数几何参数随机变量均被处理为正态分布，仅混凝土保护层厚度被认为不拒绝对数正态分布。对于同一几何参数随机性处理方式的不同，可能由于不同时期或者不同地区构件加工工艺、材料生产工艺不同所导致。在进行具体研究时，应根据待分析对象的具体情况对几何参数随机性处理方式进行确定。

表3 几何参数分布类型及统计参数下载原图

4.3 材料特性模式不确定性

通常情况下，材料强度的概率分布不拒绝正态分布或对数正态分布，材料强度标准值取值方法为:相应概率分布的0.05分位值，对应的保证率为95%，材料弹性模量、泊松比等物理性能指标的标准值取为相应概率分布的0.5分位值。文献[23]同时给出了混凝土立方体试件抗压强度标准值以及钢筋时间抗拉强度标准值的统计特性。进一步对已有研究中的材料特性取值方法进行总结，具体如表4所示。

4.4 广义抗力及广义荷载效应不确定性

截止目前的公路混凝土桥梁正常使用极限状态可靠度研究中，广义抗力不确定性的处理方式包括三种:(1)处理为常数;(2)处理为随机变量;(3)处理为模糊随机变量。前两种处理方式在当前研究中的应用最为广泛。以预应力混凝土构件可靠度分析中较为常用的σpc不确定性处理为例，预应力筋张拉控制应力σcon变异系数通常取为0.0365，预应力损失总量变异系数可偏保守取为0.15，进一步考虑预应力损失总量占据张拉控制应力的30%，通过分析计算可得到σpc变异系数为0.08，根据文献[36]的研究，σpc不拒绝正态分布。

表4 材料参数分布类型及统计特性下载原图

然而正如引言中所述，正常使用极限状态的失效准则的定义往往具有模糊性，从根本上说，正常使用极限状态失效事件属于一种模糊随机事件，所以在孙晓燕等的研究中，认为将广义抗力处理为模糊随机变量似乎更符合客观实际。然而若直接将广义抗力处理为模糊随机变量并应用于可靠度分析，缺陷有二:(1)失效概率的求解公式中被积函数是不可积的，必须借助数值积分方法;(2)分析结果仅能体现失效概率，无法获得与之对应的验算点信息。鉴于此，孙晓燕等提出采用当量随机化方法对模糊随机变量进行处理，以一个等效的均匀分布代替原有的模糊随机变量开展可靠度分析计算工作。

对于广义荷载效应的处理，各国规范在校准、修订过程中均对特定基准期内的荷载效应模型开展了大量研究，当荷载观测数据不足以建立相应的概率模型时，可参考该类研究成果。若观测数据充足，尤其研究对象具有显著地域特性时，可通过分析对广义荷载效应的不确定性进行概率度量。以裂缝宽度广义荷载效应的随机性处理为例，我国规范制定过程中以重庆交通大学1331根部分预应力混凝土梁的裂缝宽度实测数据为基础对其概率特性进行统计，发现裂缝宽度不拒绝对数正态分布。

5 正常使用极限状态可靠度分析方法

正常使用极限状态下的构件力学分析，通常情况下可采用线性理论，必要时可采用非线性理论进行分析。根据JCSS及赵国藩等前期的研究成果，对于类似正常使用极限状态可靠度指标较低的情形，分析结果对变量的具体分布类型并不敏感。因而，在关于公路混凝土桥梁正常使用极限状态可靠度的早期研究中普遍采用了中心点法进行可靠度指标计算。随着对各类不确定性因素的认知不断深入、各类参数实测及统计参数的不断积累，在明确随机变量分布类型的基础上，验算点法在后续研究中亦被应用于正常使用极限状态的可靠度分析。在最近的研究中，Cheng综合人工神经网络、一次二阶矩及重要性抽样等的优势，提出了一种更加高效的正常使用极限状态可靠度分析方法。

6 未来研究展望

截止目前，尽管国内外研究人员已在公路混凝土桥梁正常使用极限状态可靠度研究领域进行了大量的探索并取得了一定的积累。但综合当前研究现状并联系工程实践对相关研究成果的需求，仍有存在以下需要进一步深入探索的内容:

(1)同一构件不同类型正常使用极限状态功能函数可靠度对比分析

正如第4节所述，混凝土构件正常使用性能保障可能对应于多种不同类型的功能函数，现有研究中已对每一种功能函数的可靠度分别进行了探索，然而，究竟哪种指标所对应的功能函数所得到的正常使用极限状态可靠度是最不利的，在正常使用极限状态设计时，应对哪一种指标对应的可靠度水平进行控制，仍有待于进一步探索。

(2)不确定性因素认知完善

经过近20年的努力，多数随机变量及不确定性因素的统计特性已被成功认知，但鉴于正常使用极限状态功能函数展开之后的复杂性以及对正常使用极限状态失效准则的模糊性，仍需要借助大量的试验研究，通过试验数据的积累与统计分析，完善研究人员的主观认知，提升可靠度分析的准确性。

(3)正常使用极限状态可靠度分析方法提升

现有关于正常使用极限状态可靠度的研究中主要借助一次二阶矩方法中的中心点法或验算点法，少数研究中引入了蒙特卡洛方法，但与承载能力极限状态下的可靠度分析方法相比，其分析方法仍比较匮乏。随着所关注的正常使用极限状态功能函数愈加复杂，以及出于静态可靠度向动态可靠度分析迈进的考虑，有必要对正常使用极限状态可靠度分析方法进行全面提升。

(4)基于正常使用极限状态可靠度分析的设计方法完善

尽管我国现行桥梁设计规范已达到水准II的层次，但相比于承载能力极限状态下的结构设计方法，正常使用极限状态下的结构设计方法仍存在大量的简化处理，正常使用极限状态设计目标可靠度指标、分项系数校准等工作仍需要在相关研究成果的基础上作进一步完善。

(5)基于正常使用极限状态可靠度分析的既有结构评估方法

结构评估工作中，在保证安全性的前提下，尚应进一步考虑结构的耐久性，例如大件运输车辆过桥的通行评估。已有关于正常使用极限状态可靠度的研究多集中于结构设计、既有规范的可靠度校准以及服役期内某一控制指标下的可靠度分析，尚未形成基于正常使用极限状态的结构评估方法体系，公路混凝土桥梁结构服役期间正常使用极限状态目标可靠度指标的选择亦有待于进一步讨论。

7 结语

为进一步明确公路混凝土桥梁正常使用极限状态可靠度研究方向，并为后续研究以及桥梁设计、评估、维护等工作提供参考，对自上世纪80年代中期以来的相关研究进行总结梳理，综述内容主要包括:(1)现行规范中对正常使用极限状态可靠度分析的相关规定;(2)公路桥梁结构正常使用极限状态目标可靠度指标;(3)正常使用极限状态可靠度分析失效准则及功能函数建立;(4)计算模式、几何参数、材料特性、广义抗力及广义荷载效应等不确定性因素处理方法;(5)正常使用极限状态可靠度分析方法。结合现有研究现状以及实际工程的需求，对该领域下一步的研究方向及重点进行展望，依次为:(1)同一构件不同类型正常使用极限状态功能函数可靠度对比分析;(2)不确定性因素认知完善;(3)正常使用极限状态可靠度分析方法提升;(4)基于正常使用极限状态可靠度分析的设计方法完善;(5)基于正常使用极限状态可靠度分析的既有结构评估方法。

参考文献

[1] XU T,CASTEL A,GILBERT R I.On the reliability of serviceability calculations for flexural cracked reinforced concrete beams.Structures,2018,13:201-212．

[2] GHASEMI S H,NOWAK A S.Target reliability for bridges with consideration of ultimate limit state.Engineering Structures,2017,152:226-237．

[3] ZANINI M A.Structural reliability of bridges realized with reinforced concretes containing electric arc furnace slag aggregates.Engineering Structures,2019,188:305-319．

[4] GB 50153-2008，工程结构可靠性设计统一标准．

[5] QIN Q,ZHAO G.Calibration of reliability index of RC beams for serviceability limit state of maximum crack width.Reliability Engineering and System Safety,2002,75:359-366．

[6] VAL D V,Chernin L.Serviceability Reliability of Reinforced Concrete Beams with Corroded Reinforcement.Journal of Structural Engineering,2009,135:896-905．

[7] ELLINGWOOD B,TALLIN A.Structural serviceability:floor vibration.Journal of Structural Engineering,1984,110(2):401-418．

[8] 赵国藩，李云贵．混凝土结构正常使用极限状态可靠度模糊概率分析．大连理工大学学报，1990,30(2):177-184．

[9] 贡金鑫．钢筋砼构件裂缝控制的可靠度分析．西北建筑工程学院学报，1993,1:23-27．

[10] STEWART M G.Concrete workmanship and serviceability reliability.Proceeding of the 14thAustralasian Conference on the Mechanics of Structures and Materials,Horbat,Australia,1995．

[11] STEWART M G.Serviceability reliability analysis of reinforced concrete structures.Journal of Structural Engineering,1996,122:794-803．

[12] PICARD A,MASSICOTTE B.Serviceability design of prestressed concrete bridge.Journal of Bridge Engineering,1999,4(1):48-55．

[13] 江胜华，侯建国，何英明．考虑预应力损失的CRFP布加固钢筋混凝土桥梁正常使用极限状态可靠度研究．土木工程学报，2015,48(11):36-43．

[14] 姚继涛，宋璨，刘伟．混凝土受弯构件裂缝控制的可靠度分析．土木工程学报，2017,50(3):28-34．

[15] HONFI D,MARTENSSON A,THELANDERSSON S.Reliability of beams according to Eurocodes in serviceability limit state[J].Engineering Structures,2012,35:48-54．

[16] CHENG J.Serviceability reliability analysis of prestressed concrete bridges.KSCE Journal of Civil Engineering,2013,17(2):415-425．

[17] GHASEMI S H,NOWAK A S.Reliability analysis for serviceability limit state of bridges concerning deflection criteria.Structural Engineering International,2016,26(2):168-175．

[18] JTG 3362-2018，公路钢筋混凝土及预应力混凝土桥涵设计规范．

[19] CASTEL A,VIDAL T,FRANCOIS R.Finite-element modeling to calculate the overall stiffness of cracked reinforced concrete beams.Journal of Structural Engineering,2012,138(7):889-898．

[20] CASTEL A,GILBERT R I,RANZI G.Instantaneous stiffness of cracked reinforced concrete including steel-concrete interface damage and long-term effects.Journal of Structural Engineering,2014,140(6):04014021．

[21] JTG D62-2004，公路钢筋混凝土及预应力混凝土桥涵设计规范．

[22] American National Standard.Minimum design loads for buildings and other structures.SEI/ASCE 7-05,2005．

[23] GB/T 50283-1999，公路工程可靠度设计统一标准．

[24] JCSS.Probabilistic model code.Joint Committee on Structural Safety,2000．

[25] ISO 2394.General Principles on Reliability for Structures(4th E-dition).Switzerland,Geneva,2015．

[26] EN1990.Basis of structural design.Brussels:CEN;2000．

[27] LENNER R,VILJOEN C,NIEROP S V.A comparative study of target reliability index derivation for reinforced concrete structures governed by serviceability limit state.Structural Concrete,2019,20:670-677．

[28] 张士铎，张启伟．公路桥梁钢筋混凝土构件正常使用极限状态的可靠度度分析．中国公路学报，1992,5(4):26-39．

[29] 孙晓燕，黄承逵．既有钢筋混凝土桥梁正常使用极限状态可靠度分析．湖南大学学报(自然科学版)，2006,33(4):21-25．

[30] 焦美菊，孙利民．基于最大裂缝宽度的钢筋混凝土桥梁可靠度分析．工程力学，2010,27(Sup.I):245-249

[31] 赵羽习．混凝土结构粘结性能和耐久性研究．杭州:浙江大学，2001．

[32] 赵羽习，金伟良．正常使用极限状态下混凝土结构构件可靠度的分析方法．浙江大学学报(工学版)，2002,36(11):674-679．

[33] 王深，张伟平，张誉．从混凝土纵向裂宽预测钢筋界面损失的研究[C]//中国土木工程学会第九届年会学术讨论论文集，北京，2000．

[34] 孙博，肖汝诚，郭健．碳化概率模型及混凝土结构碳化失效概率分析．土木工程学报，2018,51(5):1-7．

[35] 潘钻峰，吕志涛．基于不确定性分析的大跨PC箱梁桥后期备用束设计．建筑科学与工程学报，2010,27(3):1-7．

[36] 王磊，张旭辉，马亚飞，等．混凝土梁后张预应力损失的概率特征及敏感性评估．安全与环境学报，2012,12(5):204-210．

[37] 李扬海，鲍卫刚，郭修武，等．公路桥梁结构可靠度与概率极限状态设计．北京:人民交通出版社，1997．

[38] 张喜刚．公路桥梁汽车荷载标准研究．北京:人民交通出版社，2014．

[39] 赵少杰，任伟新．公路桥梁车辆荷载截尾分段概率模型及应用．中国公路学报，2017,30(6):260-267．

[40] 赵国藩，曹居易，张宽权，等．工程结构可靠度．北京:科学出版社，2011.

声明：我们尊重原创，也注重分享。有部分内容来自互联网，版权归原作者所有，仅供学习参考之用，禁止用于商业用途，如无意中侵犯了哪个媒体、公司、企业或个人等的知识产权，请联系删除，另本头条号推送内容仅代表作者观点，与头条号运营方无关，内容真伪请读者自行鉴别，本头条号不承担任何责任。

桥梁钢筋保护层厚度规范要求(公路混凝土桥梁正常使用极限状态可靠度研究综述)

桥梁钢筋保护层厚度规范要求(公路混凝土桥梁正常使用极限状态可靠度研究综述)

刘经伟 代攀 陈军刚 涂莹莹 许鹏 何能

云南省交通规划设计研究院有限公司 云南通衢工程检测有限公司 重庆市市政设计研究院

1 正常使用极限状态分析相关规定

1.1 变形分析及控制方法

1.2 裂缝分析及控制方法

1.3 预应力构件应力分析及控制方法

2 公路桥梁结构正常使用极限状态目标可靠指标

2.1 基准期

2.2 目标可靠指标

3 正常使用极限状态失效准则及功能函数

3.1 挠度

3.2 应力水平

3.3 横向抗裂度

3.4 横向裂缝宽度

3.5 纵向抗裂度

3.6 纵向裂缝宽度

3.7 碳化深度

4 不确定性因素处理方法

4.1 计算模式不确定性

4.2 几何参数模式不确定性

4.3 材料特性模式不确定性

4.4 广义抗力及广义荷载效应不确定性

5 正常使用极限状态可靠度分析方法

6 未来研究展望

7 结语

参考文献

刘经伟代攀陈军刚涂莹莹许鹏何能

云南省交通规划设计研究院有限公司云南通衢工程检测有限公司重庆市市政设计研究院