时温等效应用(基于CEMA 计算方法的压陷滚动阻力系数影响因素分析)

Posted 2023-05-28

篇首语：人之相识，贵在相知；人之相知，贵在知心。本文由小常识网(cha138.com)小编为大家整理，主要介绍了时温等效应用(基于CEMA 计算方法的压陷滚动阻力系数影响因素分析)相关的知识，希望对你有一定的参考价值。

时温等效应用(基于CEMA 计算方法的压陷滚动阻力系数影响因素分析)

杨俊1 宋冠霆2 宋伟刚3
1 北方重工集团有限公司沈阳 110141 2 中煤科工集团沈阳设计研究院有限公司沈阳 110015
3 东北大学机械工程与自动化学院沈阳 110819

摘要：带式输送机压陷滚动阻力的确定是带式输送机设计中的重要问题。对压陷滚动阻力的产生机理进行了分析，明确了压陷滚动阻力的确定可划分为输送带压陷变形模型和材料模型两个部分，通过Jonkers 的压陷滚动阻力计算模型展示了托辊直径、输送带下覆盖层厚度等因素的影响趋势。将CEMA 小试样压陷滚动计算式转化为压陷滚动阻力系数计算式，分析了载荷变化、带速变化和温度变化等因素的影响。得出在常温条件下，压陷滚动阻力系数随载荷增加而增加、随温度增加而减小；在高带速条件下，带速对压陷滚动阻力系数几乎没影响；CEMA7 的小
试样计算方法并不能直接得到实际的压陷滚动阻力系数，尚需要根据大试样的测试结果进行正，但所反映的变化趋势将对输送带的配方设计及其选用具有指导意义；CEMA7 的载荷修正系数没有完全考虑实际输送物料在输送带上的分布，其计算结果存在一定的偏差等结论，对带式输送机的输送带选用具有重要的参考价值。

关键词：带式输送机；压陷滚动阻力；主曲线；耗散正切

中图分类号：TH222 文献标识码：A 文章编号：1001-0785（2018）10-0128-06

带式输送机压陷滚动阻力约占阻力的60% 左右[1]，尽管实际压陷滚动阻力依具体带式输送机的设计与使用条件不同所占比例有所变化，但足以说明准确确定压陷滚动阻力的重要性。压陷滚动阻力确定方法的研究延续了半个多世纪，国外著名研究者有：Jonkers、Spaans、Lodewijks、Qiu 和Rudolphi 等，国内辽宁工程技术大学、中国矿业大学、太原科技大学等也开展了相关研究，但受测试设备的限制，研究进展缓慢。

2005 年美国输送机制造商协会的设计指南给出了压陷滚动阻力计算方法[2]，但计算模型过于简化，2014年，CEMA7[3] 根据后续的研究成果改进了计算方法。本文将结合CEMA7 的压陷滚动阻力计算方法，计算压陷滚动阻力系数，给出压陷滚动阻力的影响因素，为带式输送机设计与研究人员提供定性的参考。

1 压陷滚动阻力产生的机理
物料和输送带的重力将传递到托辊上，此时，处在托辊和作为抗拉元件的输送带骨架之间的输送带橡胶将受到挤压。当输送带接触托辊组辊子表面时，挤压力引起输送带变形，并阻碍输送带的运动。相反，输送带通过托辊后，由于恢复作用，挤压变形将减小。由于橡胶是粘弹性材料，挤压变形的恢复存在时滞，变形功的一部分不能恢复。导致这部分变形能全部转化为热能而损耗，这可以看成由作用辊子中心和垂直反力中心之间的偏距产生的沿输送带运行方向的纯运动阻力，如图1。压陷滚动阻力确定方法可分为大试样和小试样方法。小试样方法本质上是基于输送带橡胶覆盖层的力学性能，通过建立压陷滚动阻力计算数学模型的数值。取3mm×12 mm×30 mm 输送带下覆盖层试样，其主要处理的问题是：
1）输送带压陷变形模型，取决于带式输送机托辊承载输送带和物料的几何参数、载荷、边界条件和如何处理材料变形的动能；
2）材料模型，与材料性质的本构关系，即橡胶覆盖层的应力- 应变关系。
Jonkers[4] 首先给出了基于输送带下覆盖层橡胶的主曲线的压陷滚动阻力计算方法，采用输送带与托辊接触的一维文克勒（Winkler）变形模型，并假设输送带与托辊的接触为对称的，输送带的接触应变按半正弦变化，其压陷滚动阻力系数J f 可以表示为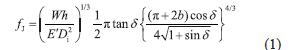

式中：w 为胶带单位宽度正压力( 由输送带和物料作用引起)，N/mm；δ 为橡胶的损耗角，应变滞后应力的角度，º； h 为输送带下覆盖层厚度，mm； 0 E 为橡胶的储存模量，N/mm2； i D 为托辊直径，mm； b 为输送带与托辊的接触宽度，mm。
输送带经过托辊与托辊的接触频率为

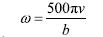
式中： v 为带速，m/s。
一般认为，Jonkers 模型过于简化，由于采用稳态过程能量相等关系确定压陷滚动阻力，缺少瞬态项，所计算出的压陷滚动阻力值偏高( 实际上，采用小试样方法确定的压陷滚动阻力远低于实际值)。一些学者认为Jonkers 模型违背粘弹性本构关系是误解。其所得结果：压陷滚动阻力系数与tanδ / E′1/3成正比，与单位宽度正压力W1/3、覆盖层厚度h1/3成正比，与托辊直径D2/3成反比，该结果已经得到广泛认同。

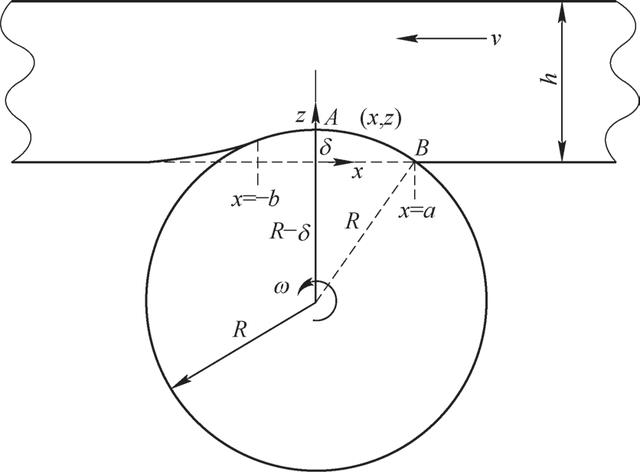
图1 输送带经过辊子的变形

2 CEMA 小试样方法
CEMA 计算方法是由Rudolphi[5-8] 等开发的，在输送带下覆盖层材料的粘弹性采用广义Maxwell 模型的基础上，研究了加入炭黑橡胶的应力- 应变的非线性关系，并结合压陷滚动阻力确定的有限元方法的研究成果，采用大试样的测试结果进行修正，较好地反映了压陷滚动阻力的研究成果。

尽管CEMA 计算方法可以采用英制单位和国际单位制计算，但由于英制单位表达复杂，实际计算中存在英制单位和国际单位制混用的情况。将CEMA7 的小试样计算方法整理如下( 所用符号不是原文符号)，除主曲线转移量的计算采用国际单位制外，其他各计算式均采用英制单位。
小试样方法的压陷滚动阻力系数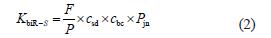

式中： biR-S K 为小试样方法的输送带覆盖橡胶的粘弹性特征； jn P 为从一维文克勒变形模型导出的与输送带性能无关部分； F 为与耗散有关的正则系数； P 为与储存有关的正则系数； bc c 为输送带骨架修正系数，织物骨架为1.2，钢丝绳芯输送带为1.12； sd c 为一维模型修正系数，2.0； 0 E 为输送带覆盖层弹性模量，磅/ 英尺2；W 为在带宽上的单位宽度正压力，磅/ 英尺。

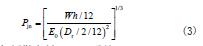
2.1 确定与耗散有关的正则系数
输送带与托辊的接触系数

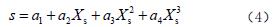
式中： s X 为物料和输送带作用在托辊上的最大压力与计算基准最大压力的转换系数。
耗散主曲线转移量

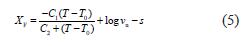
式中： u v 为带速，m/s， u v ×0.304 8 / 60，单位变为英尺/min。
式(5) 中的第1 项为WLF 时温等效原理的主曲线的转移量，第2 项和第3 项是由于带速和接触宽度引起的接触频率的主曲线转移量。

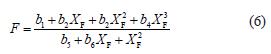
以上各式中： i i 1 2 a、b C C 和0 T 为与橡胶覆盖层性能有关的常数，见CEMA7 表6.47。

2.2 确定与存储有关的正则系数

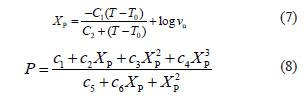
常数i c 见CEMA7 表6.48。
应用上面的计算式，给出压陷滚动阻力系数与载荷、带速和温度变化的关系曲线，如图2 ～图5，其中1 为低滚动阻力输送带、2 为常用输送带、3 为适用于低温输送带、4 为CEMA6 中所给参数的输送带。从图2 中可见压陷滚动阻力系数随载荷的增加而增加，这也可以从Jonkers 模型看到。图中计算结果托辊直径为159mm，输送带下覆盖层厚度为8 mm。从图3 可见，压陷滚动阻力系数随带速变化不明显，特别是高速段，这是由于带速的增加相当于接触频率增加，但是在高速区带速增加所引起的频率增加的相对值小，而在低速段带速增加较小的量也会引起接触频率明显增加。一些作者在没有考虑橡胶特性的前提下给出的压陷滚动阻力随带速的增加而增加是片面的。一般认为当频率增加一个数量级相当于温度变化7℃。在输送带的高弹性区，频率的变化对耗散正切的变化影响较小。这也是图3 中低滚动阻力输送带的压陷滚动阻力系数几乎不随带速变化的原因。

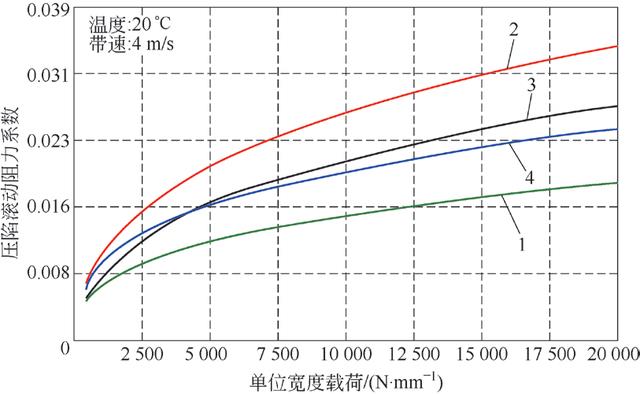
图2 压陷滚动阻力系数随载荷变化曲线

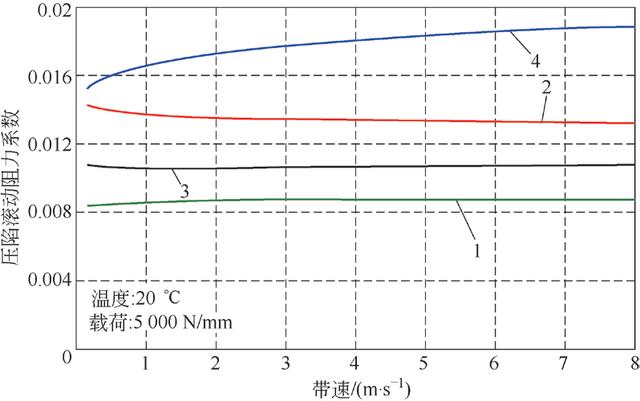
图3 压陷滚动阻力系数随带速变化曲线

从图4 和图5 可以看出，适用于低温输送带在零下12℃左右开始，压陷滚动阻力系数随温度的降低而减小，而低滚动阻力输送带在低温条件下却大幅度增加。一些作者所给出的压陷滚动阻力随温度降低而减小的结论是片面的。从橡胶的主曲线和耗散正切曲线来看，存在一个耗散正切最大值的温度，该温度对应了橡胶的玻璃化温度，当橡胶的工作频率和温度效应的共同作用达到玻璃化后，压陷滚动阻力系数将减小。而尚未达到低滚动阻力输送带的玻璃化温度，压陷滚动阻力系数增加较多。

3 CEMA 大试样方法
大试样测试方法是将输送带取样为400 mm 的带条，构成闭环系统，用以测定输送带的下覆盖层的压陷滚动阻力。实验过程中，实验台放置于温度可调的环境中，通过测试辊施加载荷，可以对一种覆盖层配方分别测出不同带速、载荷、托辊直径、环境温度下的压陷阻力，

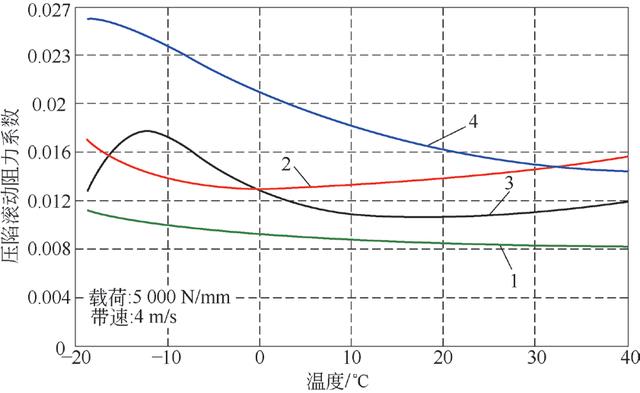
图4 压陷滚动阻力系数随温度变化曲线1

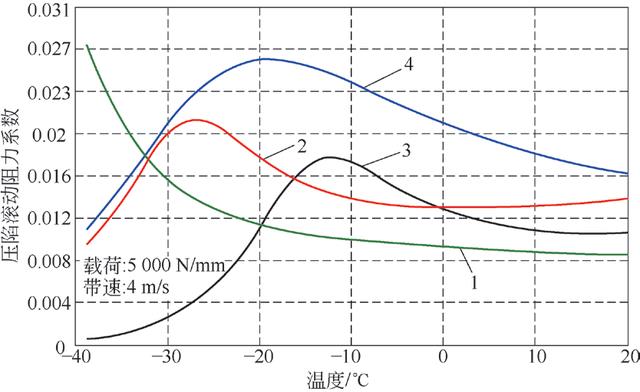
图5 压陷滚动阻力系数随温度变化曲线2

在实际测试中，需要去除托辊旋转阻力、输送带弯曲阻力等影响因素。已经开发出了多种测试设备，Hanover大学最早开发了压陷滚动阻力实验台，并形成了DIN22123—2012[9]，Newcastle 大学的Wheeler 设计了简易的实验台，并通过改进设计了新实验台，形成了AS1334.13—2017[10]。尽管通过这两个实验台能够得出压陷滚动阻力，但是在考虑施加均匀载荷时，尚需要根据输送带和物料在托辊组辊子上的载荷分布假设计算压陷滚动阻力。由于大试样的方法来自于Hanover 大学或Newcastle 大学的测试结果，其压陷阻力的计算可直接采用国际单位制。

CEMA 大试样方法是在实验台上直接施加载荷和改变温度，确定出压陷滚动阻力或压陷滚动阻力系数，再根据理论研究结果对压陷滚动阻力系数进行修正。

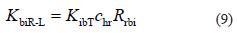
式中： biR-L K 为大试样方法的输送带覆盖橡胶的粘弹性特征。
对于大试样方法，为确定单位载荷的压陷损耗，定义一个新变量biT K ，它是由大试样方法确定的。大试样方法的压陷滚动阻力系数的实验值为biT K 。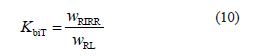

式中： biT-L K 为大试样方法压陷滚动阻力系数； RIRR w为单个托辊辊子的压陷损耗，N/mm； RL w 为单位宽度载荷，N/mm。

大试样方法使用的RL w 看作运行托辊通过测试辊子作用在输送带上的平均线载荷，其测试结果见CEMA7表6.61。
对托辊直径和覆盖层厚度的修正系数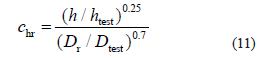

式中： test D 为测试设备上的托辊辊子直径，mm；test h 为测试输送带的下覆盖层厚度，mm。此关系式可直接从式(1) 得出。

应用CEMA7 中的参数，大试样方法的两种输送带压陷滚动阻力随载荷、温度的变化关系如图6 和图7。测试条件：托辊直径为219 mm，输送带下覆盖层厚度为7 mm。

大试样方法考虑了温度、载荷大小、输送带覆盖层厚度与托辊直径的影响，按照对压陷阻力的有限元方法的分析结果，带芯部分也会对压陷滚动阻力产生影响，小试样方法的计算模型不包括带芯部分，是通过输送带骨架修正系数来考虑的，然而，输送带下覆盖层厚度变化时，此修正系数应随厚度变化而变化。在大试样方法中没有考虑这一影响。

由于CEMA7 的大试样和小试样压陷滚动阻力确定方法采用的是不同橡胶覆盖层配方，压陷滚动阻力系数没有可比性。但值得注意的是，小试样方法所得的压陷滚动阻力系数是修正后( 输送带骨架修正系数为1.12，一维模型修正系数为2) 的数值，与大试样方法的结果基本相当。可以认为，当前研究水平下的小试样方法所得压陷滚动阻力系数与实际值相比偏小，且不应得出小试样方法的结果与大试样的测试结果相近的结论。事实上，小试样方法的修正系数是大试样的测试结果给出的。

4 CEMA7 的压陷滚动阻力计算
物料和输送带作用在托辊上的最大压力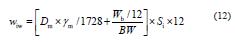

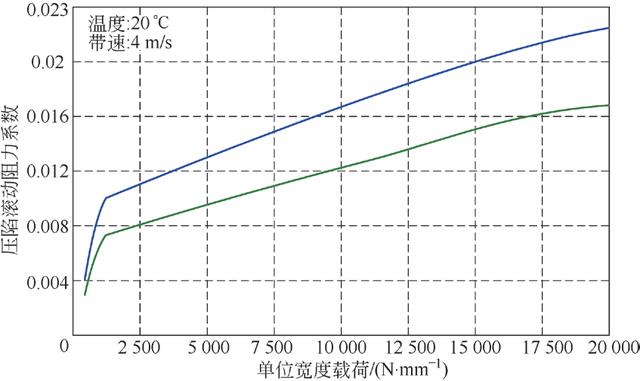
图6 压陷滚动阻力系数随载荷变化曲线

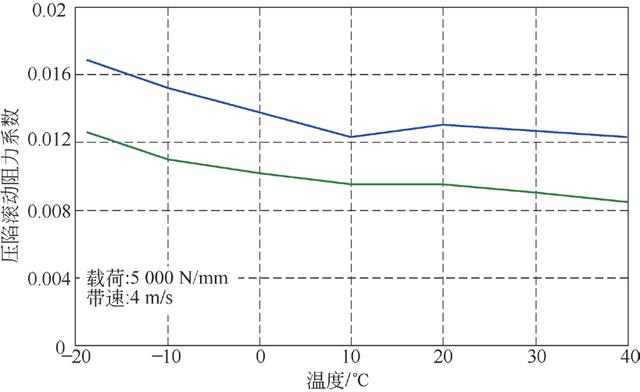
图7 压陷滚动阻力系数随温度变化曲线

式中： iw w 为物料和输送带作用在托辊上的最大压力； m γ 为物料密度，kg/m3； i S 为托辊间距，m， m D 为物料最大堆积深度，英寸。

物料和输送带作用在托辊上的最大压力与计算基准最大压力的转换系数s X

式中： max W 为基准最大压力，50 000 N/m。物料最大堆积深度可根据实际输送量和物料堆积截面进行计算，并将式(3) 中的W 替换为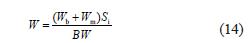

式中： b W 为输送带单位长度质量，N/m； m W 为物料单位长度质量，N/m， BW 为带宽，mm。
区段的压陷滚动阻力为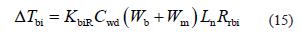

截面积A 和表示修正的平均线载荷iw w 的修正系数wd C 为

式中： bi ΔT 为压陷滚动阻力； wd C 为载荷分布系数；rbi R 为修正系数； Id X 为载荷压力调整系数； n L 为区段长度，英尺；β 为槽角，º； s φ为安息角，º。

这里存在一个矛盾，计算物料和输送带作用在托辊上的最大压力iw w 时，是通过物料的实际输送量来确定的。而式(16) 却没有具体体现实际输送量下的物料在输送带上分布对修正系数wd c 的影响，因为物料与侧辊的接触长度直接受输送量的影响。CDI 的Jennings 也对式(16) 提出了质疑[11]。压陷阻力的计算可参见CEMA7 中的算例。

5 结论
本文对CEMA 压陷滚动阻力系数计算方法进行了分析，介绍了Jonkers 模型的计算方法，所得结论如下：
1）在常温条件下，压陷滚动阻力系数随载荷增加而增大、随温度提高而减小；在高带速条件下，带速对压陷滚动阻力系数几乎没有影响。
2）CEMA7 的小试样计算方法并不能直接得到实际的压陷滚动阻力系数，尚需要根据大试样的测试结果进行修正，但所反映的变化趋势对输送带的配方设计及其选用具有指导意义。
3）CEMA7 的载荷修正系数没有完全考虑实际输送物料在输送带上的分布，其计算结果存在一定的偏差。

参考文献
[1]Hager M, Hintz A. The Energy Saving Design of Beltsfor Long Conveyor Systems[J]. Bulk Solids Handling.1993， 13(4): 749-758.
[2]CEMA. Belt Conveyors for Bulk Materials[M]. 第6 版.Florida: The Conveyor Manufacturers Association,2005.

[3]CEMA. Belt Conveyors for Bulk Materials[M]. 第7 版.Florida: The Conveyor Manufacturers Association,2014.
[4] Jonkers C. The Indentation Rolling Resistance ofBelt Conveyors: A theoretical approach[J]. Fördernund Heben, 1980，30(4): 312-318.
[5]Rudolphi T,Reicks A. Viscoelastic Indentation andResistance to Motion of Conveyor Belts using a GeneralizedMaxwell Model of the Backing Material[J].Rubber Chemistry and Technology, 2006，79(2): 307-319.
[6]Rudolphi T J. Applied Rubber Belt Cover Loss Predictionfrom Indentation[M]. 2008.
[7]Rudolphi T, Reicks A.The Importance of NonlinearStrains Considerations in Belt Cover IndentationLoss[J]. Bulk Solids Handling，2012，32(2): 52-57.
[8]Rudolphi T, Reicks A, Wheeler C. A Comparison ofCalculated and Measured Indentation Losses in Rubber Belt Covers[J]. Bulk Solids Handling, 2012，
32(3): 52-57.
[9]Normenausschuss Bergbau (FABERG) im DIN .Conveyor belts – Indentation rolling resistances of conveyor belts related to beltwidth – Requirements,testing DIN 22123—2012[M]. Berlin: Beuth VerlagGmbH，2012.
[10]AS 1334.13—2017 RU-002—Conveyor and Elevator Belting.Methods of testing conveyor and elevator belting - Method 13: Determination of indentation rolling resistance of conveyor belting[S]. Sydney: Standards Australia，2017.
[11]Jennings A.The CEMA Horsepower Equation: Development of a new conveyor power prediction methodology[J]. Bulk Solids Handling，2014，34( 特刊)：34-40.

时温等效应用(基于CEMA 计算方法的压陷滚动阻力系数 影响因素分析)

时温等效应用(基于CEMA 计算方法的压陷滚动阻力系数 影响因素分析)

时温等效应用(基于CEMA 计算方法的压陷滚动阻力系数影响因素分析)

时温等效应用(基于CEMA 计算方法的压陷滚动阻力系数影响因素分析)