日本图纸△代表什么(隐藏在日本家纹中的数学)

Posted 2023-05-28

篇首语：鞭打的快马，事找的忙人。本文由小常识网(cha138.com)小编为大家整理，主要介绍了日本图纸△代表什么(隐藏在日本家纹中的数学)相关的知识，希望对你有一定的参考价值。

日本图纸△代表什么(隐藏在日本家纹中的数学)

女士们，先生们，老少爷们儿们！在下张大少。

日本家纹是一种简单的圆形图案，许多日本家族都有与他们家族相关的设计。玩过日本游戏《信长之野望》的朋友想必都对满地图的家纹图案印象颇深。这些设计中的许多都可以用直尺圆规来创作。在这篇文章中，我讨论了日本文化、几何和对称性在这些常见设计中的联系，以及我在起草这些设计时的探索。

家纹是日本的徽记或徽章，通常与宗族或机构有关，呈圆形排列，如图1所示。家纹类似于欧洲的盾牌，被用来点缀各种物品，从战旗和盔甲到衣服等日常物品。家纹设计的简洁和热衷于圆形使得这些设计在数学上非常美丽和有趣。

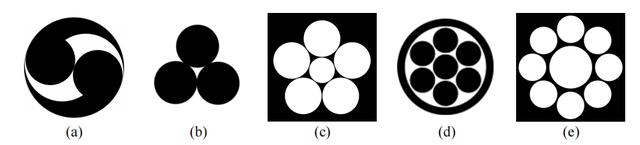
图1：具有不同对称性的家纹设计的例子

家纹的对称性

二重对称是家纹中最常见的对称。二重对称可能很受欢迎，因为家纹与切割模板的关系，因为二重对称设计只需要一折纸就可以切割设计。紧随其后的是三重和五重对称，可能是因为樱花或木莓等图案中使用的日本植物更有可能具有奇数阶的对称。另一个可能的原因是，在日本文化中，人们偏爱奇数，这是在社会上展示的，比如以奇数购买物品或赠送礼物，因此也会体现在艺术和设计中。

图2是我对参考文献[1]中所有家纹设计的统计，其中Dn表示第n个二面体群，Cn表示第n个循环群。有的对称性非常罕见，我找不到一个例子是7重、9重和11重对称。对称性超过10重的设计要么是12重，要么是16重。可能对称度高于10重的设计并不多，因为这些设计往往印在直径1至2英寸的织物上，所以对称数高的设计在视觉上会模糊不清。鉴于此，人们可能会想，在日本家纹设计中，某些n重对称的出现或缺乏或许与正n边形是否可以用圆规和直尺构造有关。

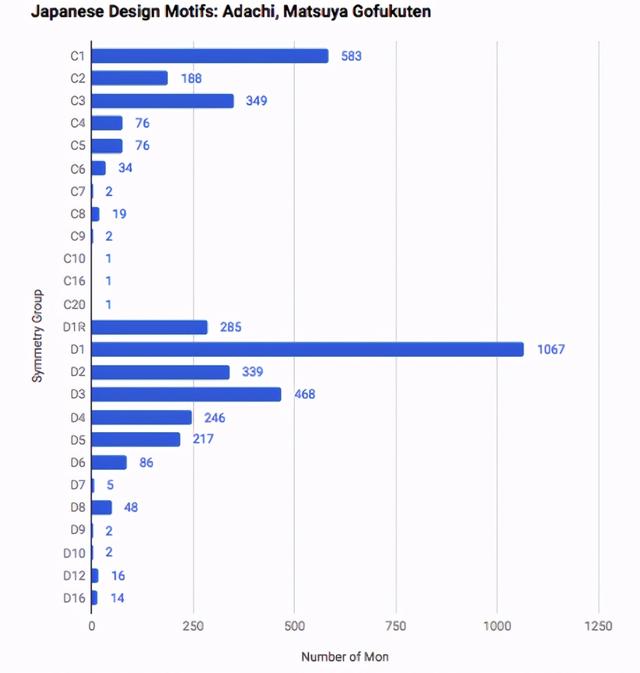
图2：根据Adachi，Matsuya Gofukuten的《日本设计主题》将家纹按照对称群（二面体群和循环群）分类

图3：用Geogebra创建的7个圆圈纹饰的尺规作图结构

尽管没有像欧几里得几何学中允许的结构那样的规则，但许多家纹的设计可以只用圆规和直尺来绘制。圆规可以自由地放在任何地方，而且不一定"可折叠"。

在圆中内接多边形

如果家纹设计需要一定的直径，比如在制作一件衣服上使用的模板时，我们应该先创建一个外圆作为设计的边界。由于许多设计以旋转或反射对称为特征，并且与二面体群或循环群相关联，因此我们接下来需要用正多边形来内切圆。正多边形应该是正n边形，其中n是设计中的n重对称。由于绘制圆内接多边形是设计的第一步，这似乎可能会限制可以用这种方式制作的设计类型。

Hatoba Shoryu是一名家纹设计师，专门从事古老的家纹绘画艺术。他的网站[4]包含了他称之为"家纹曼荼罗"的美丽作品，这些作品的特点是用圆规精确起草的弧线来设计家纹。我自己尝试用与Hatoba相同的风格来起草家纹，如图4（b），我用圆规和直尺手绘。这个设计的基础是在开始时用一个外圆来确定设计的大小，然后画上一个五边形。五边形作为放置花瓣的基础，圆形花瓣的大小近似于我从原稿中猜测的可能大小。

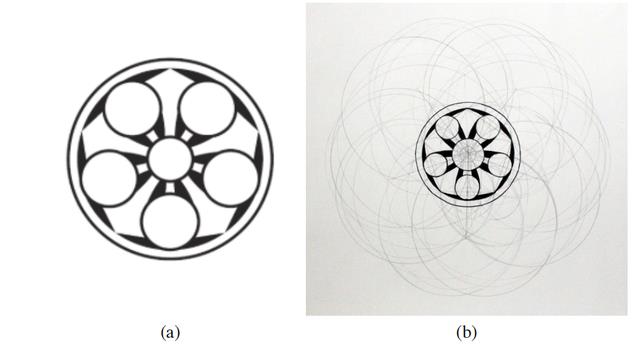
图4:梅花家纹: (a)Cindi Kusuda绘制的梅花家纹， (b)用圆规和直尺手绘出梅花家纹的变体。

切圆问题

家纹设计有成千上万种。虽然许多设计是几何的，但也有一组设计以切线圆为特征。在一些设计中，这些圆实际上并不相切，但为了起草设计，人们需要想出如何创造对称的、相切的圆，这些圆同时还与外圆相切。

最容易绘制的例子之一是图1(D)所示的圆环和7个小圆设计，其尺规作图结构如图3所示。一旦绘制了外环，要将相同半径的7个圆圈放入更大的圆圈中，需要将圆圈的直径三等分。直径的三分之一的长度形成了7个小圆的直径。一旦画出内圆，其他6个圆的放置就相当容易了，而且它们都是彼此相切的，也都是与外环相切的。这张图和图1(B)中所示的一般星形很容易画出来，因为它很容易快速地把一个正三角形画成一个圆，所以画一个正六边形也很容易。

结论

我提到发现某些对称在家纹中比其他对称更受欢迎，推测原因要么是文化上的，要么是数学上的。从数学上讲，如果大多数家纹都是用正n边形为底的圆规和直尺来设计和绘制的，那么实际上，我们就能大多数家纹构造出正n多边形的n重对称。

参考文献

[1] F. Adachi and Matsuya Gofukuten. Japanese Design Motifs: 4260 Illustrations of Heraldic Crests, New York, Dover Publications, 1976.

[2] H. Fukagawa and K. Horibe. "Sangaku-Japanese Mathematics and Art in the 18th,19th, and 20th Centuries." Bridges Conference Proceedings, Seoul, 2014, pp. 111-118. 25.

http://archive.bridgesmathart.org/2014/bridges2014-111.pdf

[3] H. Fukagawa and T. Rothman. Sacred Mathematics: Japanese Temple Geometry. Princeton University Press, 2008, pgs. 111-112.

[4] S. Hatoba. Mon-Mandala. http://www.kyogen.com/zhu_shi_hui_she_jing_yuan/bo_hu_chang_cheng_long_MON-MANDALA.html

[5] W.M. Hawley and K.K. Chappelear. Mon: The Japanese Family Crest. W.M. Hawley, 1976.

[6] I. Honda. Traditional Japanese Family Crests: For Artists and Craftspeople. Dover Publications, 2002

[7] Wikimedia Commons. https://commons.wikimedia.org/wiki/Category:Mon_(emblem)

[8] Felicia Tabing, Mathematics in Drafting Japanese Crest Designs

青山不改，绿水长流，在下告退。

转发随意，转载请联系张大少本尊。