手脑速算(魔术师怎么知道你脑中的数字的?)
Posted
篇首语:相逢意气为君饮,系马高楼垂柳边。本文由小常识网(cha138.com)小编为大家整理,主要介绍了手脑速算(魔术师怎么知道你脑中的数字的?)相关的知识,希望对你有一定的参考价值。
手脑速算(魔术师怎么知道你脑中的数字的?)
数学魔术就像读心术一样,你需要去揭示下面四个把戏背后的秘密。
数学遵循一定的逻辑。如果一种情况能够用数学来准确地描述,那么有时可以提前几个世纪预测将来必定会发生的事情——例如,月食发生的时间、七星连珠发生的时间等等。对于那些不熟悉预测背后的数学的人来说,这个结果看起来像是魔术。
接下来我们一起探索四个数学魔术的例子,它们乍一看好像是读心术,像是舞台魔术一样,会让我们想知道:“他们是怎么知道我在想什么的?”
大家应该都看过一个魔术,魔术师随机找一个观众,让她想一个数字,写下来给观众看,但只有魔术师看不到。然后魔术师对这个数字进行一系列简单的算术运算,最后,魔术师会猜到这个数字,多么令人惊奇!这是怎么做到的呢?
这里举个简单的例子,可能会让你周围的孩子大吃一惊,甚至激发他对数学的兴趣。
谜题1
这个魔术适用于可以算乘法的小孩子(如果不行,可以找人帮忙算)。让小红(或者小明)想一个三位数,但不要说出来,告诉他们你可以变出两个秘密数字。第一步,让小红把数字乘以7,然后乘以11,最后,加以适当的魔术表演与语言,再将结果乘以13。
如果她做对了,可能会发现她笑得很开心。而对你,或者对一个大一点的孩子来说,问题是——怎么做到的?
聪明的读者已经发现了,这个过程其实是将秘密数字乘以 7 × 11 × 13 = 1,001,这个数字能将原始的三位数字“复制两份”,比如说秘密数字是 457:


谜题2
在2 和 9 之间有两个未知数字,这个数字可以包含2或9,也可以是一样的。S 和 P 是两位逻辑清晰的数学家, S 知道了两个数字的和,P 知道了两个数字的积分。然后他们的对话如下:
S:我没法推断这两个数字是什么。
P:我也没法推断是什么。
S:哦,那我知道是什么了!
P:那我也知道了!
乍一看,这似乎是一种神奇的读心术——他们从哪里获得解决问题的新信息?你能找出这两个数字吗(有两个可能的答案),你能解释一下S和P是怎么做到的吗?
提示:将S和P的所有可能情况制成表格,找出在对话中可以推断的信息(记住要考虑所有可能的情况)。这并不涉及任何困难的计算,但容易混淆他们各自的信息。
这里给出一种分析:根据可能的情况绘制 8×8的表格,表格的元素用(和,积)来表示,根据两人的对话对可能的数字进行分析:

1. S说他无法推断出这些数字是什么时,意思是,他得到的和在表格中不止一次出现,去掉那些只出现一次的数字:4(2+2)、5(2+3)、17(8+9)和18(9+9),这些可以从列表中删除,并在图中显示为灰色。
2.同理,P 说他也不能推导出这些数字,说明他得到的乘积也不止出现了一次,找到出现不止一次的数字:12(2×6,3×4)、16(2×8,4×4)、18(2×9,3×6)、24(3×8,4×6)和36(4×9,6×6)。这些结果以红色显示,其他的可能都排除。
3.S可以推导出乘积。这意味着在这些乘积中,对应他的数字只有一个是可能的。因此,我们需要观察每个求和对角线,选择只有一个红色乘积的对角线。可能的情况有:积为12、18、36和36,对应的和分别为7、9、12和13(用红色箭头所示)。
4.P可以推导出和,代表只有一个和与他的乘积对应。36可以排除,因为36的总和可能是12或13。因此,唯一可选择的和积对是(7,12)和(9,18),它们对应于原始数字对(3,4)和(3,6)。
答案(3,4)和(3,6)都符合问题陈述,并且都是正确的。然而,读者达米恩表示,只有一个正确答案(3,4)。在下一个谜题中可以看到,随着可选数字上限的增加,这类谜题的答案可能会改变,如果数字的范围从9变为10,那么(3,4)仍然是一个解,但是(3,6)就不是了,所以把(3,4)看作是原始问题的稳定解,像(3,6)这样在更改数字范围时出现和消失的解,称为“幻影解”(phantom solutions)。

谜题3
现在,同样还是两个数字(可以相等),现在它们介于2和70之间。同样的,给S出两个数字之和,给P出两个数字之积,他们对话如下
P:我没办法推断这两个数字是什么。
S:我本来可以告诉你的,尽管我也不能推断出数字。
P: 哦,现在我知道这两个数字是什么了!
S: 我也是!
再次找到这两个数字是什么,S 和 P 是怎么算出来的。
谜题2中,有15个不同的和和64个不同的乘积,谜题3中,有137个和及4761个乘积。
通过列表法可以找到谜题2 的解,但是到谜题3这里,可以尝试利用电子表格或者编程来计算,一些读者无疑会这样做。但如果仔细思考S的第一句话,可以用一些初始数论的思想来限制一些可能性,从而在纸上解决这个问题。所以第二个问题是:利用数论原理,在排除一些选项之后,手动计算的最小可能情况有多少种?
这里给出参考的解决思路:
1.由于P不能推导出两个数,所以P不可能是两个素数的乘积,同样,S也不是两个素数的和。这里出现了哥德巴赫猜想,这也许是数论中未经证实的最著名的猜想了。哥德巴赫猜想指出:任一大于2的偶数都可以表示为两个素数之和。虽然这个猜想还没有证明,但是对于4 × 1018 以下的偶数都成立。因为我们猜的数的范围远小于此,因此可以肯定地说 S 不可能是偶数。
2.推导1的另一方面,我称之为推导2的是:S不可能是奇数的素数与2的和,因为2是素数。比如说S不可能是9,因为9是素数 7 与2的和,它们的乘积是14,只有一种分解:2×7,这种情况下,P会立刻知道这两个数字是什么。
3.最后,S必须小于等于2加上一个素数,这个素数是大于等于范围上限的一半的最小素数。比如范围为70时,这个素数就是大于70一半,即35的最小素数:37。根据规则,S不能大于等于39。这个条件是由乘积这一项的范围限制的。比如说,如果 S 是39,为37+2,其都是素数,会被马上推断出来,且不满足推导2。下一个奇数41,其乘积为37×4=148,分解为74×2 时,74超过范围;另一种分解37×4的可能也会马上推断出来两个数。同理,37+6,37+8,37+10……直到70。一般来说,任何大于39的奇数都可以表示为 37+X,其中X为偶数,因此这样的因子都可以被分解为 37×X 的形式。
4.根据上述推导,可以利用 S 和 P 的前三个对话将可能的数字缩减到 11, 17, 23, 27, 29, 35 和 37,这已经很棒了,但可以更进一步。S给出第四句的关键是:必须有一个唯一的乘积P对应S的和。来看 S=11 的情况,可以表示为 3+8或者3+23 也可能是7+4或7+22,如果P推导S为11,那么P可能是24,分解为3×8 的情况,S为11;另一种分解2×12的情况给出S为14,根据推导1不成立;4×6的情况S为10,同样排除。如果P为28,分解为4×7,S也为11,允许;分解为2×14,S为16,不允许。因此,给定S为11的情况下,无法确定 P 是24还是28,因此这里给出推导4:S不能为可以用 y+2n表示的形式,其中y为一个奇素数。
从目前的候选数字中来看,11已经被排除了。同理23 (19 + 4 和 7 + 16),27 (23 + 4,19 + 8 和 11 + 16),35 (31 + 4,19 + 16 ,3 + 32) 和 37 (29 + 8 和 5 + 32)也都被排除了。现在只剩下17和29这两个可能。可以排除29的选项,因为13+16、25+4都有可能,根据对话S必须只有一种选项。
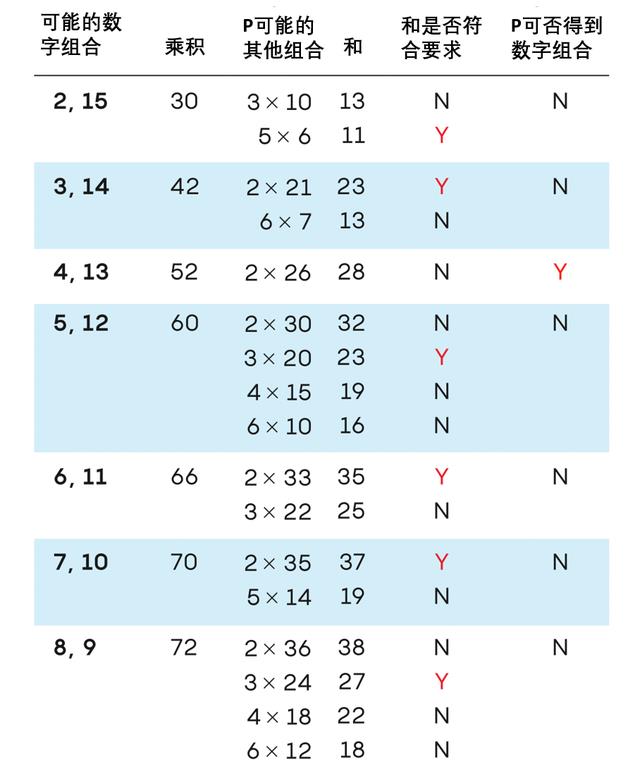
下表中给出了S=17 的可能情况,第一列有一对候选数字,第二列对应着其乘积,第三列是针对乘积给出的可能数字,第四列为对应的第三列的和。第五列代表这些和根据对话是否是允许的(其必须是11、17、23、27、29、35和37中的一个)。哪怕是第五列得到的Y,也不代表P知道这两个数字,因为第一列的一对,可能有两种数字对。结合第六列,只有一种可能,即4×13,这就是谜题唯一的答案。

谜题4
一个“数学大师”扔掉了牌里面的2到6的数字,从而准备了一副32张牌。他将剩下的牌按照一定的顺序排列,然后牌面朝下放在桌子上。随机挑选五个人坐到桌子旁,然后他们一个接一个地切牌。然后第一个人拿走最上面的牌,将牌组传递给第二个人,第二个人依次拿着当前的最上面的牌,依此类推。当每个人都有一张卡片时,最后一个人将牌组正面朝下放回桌上,然后都回到自己的座位上。
现在,表演者要求五个人以心灵感应的方式向他传送卡片。他聚精会神地皱着眉头,最后,无奈地摇了摇头。“这几天越来越难了,宇宙膨胀导致红移,干扰了我接收到的颜色。请持有红牌的人站起来好吗?”
第二个和第五个参与者站了起来。这位数学家脸上掠过一丝宽慰的神色。“现在很清楚了,你有红心10,你有方块K。”事实确实是如此,他也猜对了其他三个人的牌。
他是怎么做到的?好吧,既然我告诉过你这个把戏是严格的数学技巧,很明显他记住了卡片顺序(可能使用了某种代码),而且卡片顺序在五次随机切牌中保存了下来,你知道为什么吗?
提示:考虑序列00010111,它周期性地包含了由0和1组成的八个可能的三联数:000、001、010、101、011、111、110和100。如果你像扑克牌一样“切”它,会发生什么?
表演者在舞台上的打趣是纯粹的戏谑还是戏法的关键?当你玩这个把戏的时候,你能想出卡牌的顺序么?
这里给出一位读者提供的解法。
序列00010111称为0和1上的3阶德布鲁因(de Bruijn)序列。像扑克牌一样对它进行“切牌”就相当于把它循环若干次,与此同时,仍然保留其序列的属性。我们可以构造所有可能的由5个 B 和R构成的所有可能序列和,例如:
BBBBBRBBBRRBBRBRBBRRRBRBRRBRRRRR,
其长度为:25=32位,这跟我们卡牌数目一样,让德布鲁因序列中的每一个B对应一张黑牌,R对应一张红牌。B和R的每一种排列都是唯一的,所以一旦你知道红色在哪里,你就知道五张牌的整个顺序(BRBBR)。然后简单地记住卡牌的顺序,直到找到对应的这五张牌的顺序,你就知道答案了。在表演中,为了找到红色的牌的顺序,开玩笑的流程是必要的。

希望你能从以上谜题中的各种信息里面推断出更多的信息,这就是魔法的奥秘!去享受解开这些魔术的乐趣吧!
相关参考
1、解答过程如下:9x99=99x(100-1)=99x100-99x1=9900-99=9801。2、运用了运算定律与数字的基本性质,从而使计算简便,使一个很复杂的式子变得很容易计算出得数。3、简便计算中最常用的方法是乘法分配律。ax(b+c)=axb+axc其中a,b,c是任...
...改车漆、做街上最靓的仔!1.选对喜欢的颜色很重要!当你脑中萌生“更改车漆”这个想法的时候,恭喜你,你已经成功了一半。因为有了想法,那么就剩下的一半就是如何实施了!当然,实施起来并非那么简单,各种细节也需...
1、个位数是“1”。速算口诀:头乘头,头加头,尾是1(头加头如果超过10要进位)2、十位数是“1”。速算口诀:头是1,尾加为,尾乘尾(超过10要进位)3、个位数都是“9”。速算口诀:头数各加1,相乘再乘10,减去相加数,...
提起清宫里的太医,你脑中浮现的是下跪听旨?悬丝诊脉?是承诺护甄嬛一世周全的温太医?还是《延禧攻略》里因医术高超被招进宫廷的江湖游医叶天士?影视剧里的太医形象多是按照剧情需要而设定,清代宫廷里太医群体状...
1、由速算大师史丰收经过10年钻研发明的快速计算法,通过左手五个手指的伸和曲结合大脑的记忆进行运算的方法。这套方法打破人类几千年从低位算起的传统方法,运用进位规律,总结26句口诀,由高位算起,再配合指算,加...
1、口诀为:食指伸开“l”,中指伸开“2”,无名指为“3”,小指伸开“4”;四指一握伸拇指,拇指是“5”要记住;再伸食指到小指,“6”“7”“8”“9”排成数。2、口诀使用方法:先确定双手分工:左手代表十位数,右手...
1、被乘数的“数首”和乘数的“数尾\'、被乘数的”数尾“和乘数的”数首“相乘以后,两积相加得一数;2、被乘数的“数首“和乘数的”数首“、被乘数的”数尾“和乘数的”数尾“相乘以后,两积相加得一数;3、把以上得...
脑组织与身体其他器官不同的是,它对缺血、缺氧性损害非常敏感。只要完全缺氧超过3~5分钟,脑神经细胞就会死亡,并且不可再生。大量临床研究表明,对于脑梗死患者,真正安全有效的抢救神经细胞功能的时间是3~6个小...
晨虹油漆厂家是哪里的(今日进博丨沸水1秒变凉白开?这些居家好物让你脑洞大开)
沸水秒变凉白开?怎么做到的?11月8日,“今日进博”打开你的想象空间解锁家庭新生活最方便家中老人生病了下床很困难怎么办?松下的这款电动分离床完美解决难处一拉、一按、一推分离出去的半张床“变身”轮椅而且单人...
误区一:血压正常或偏低者不会得中风。人们都知道高血压容易得脑血管病,高血压是脑出血和脑梗死的最重要的危险因素,但不是唯一的危险因素。脑动脉硬化病人由于脑血管管腔变得狭窄,以及其他因素存在,即使血压正常...