性质的意思(《几何原本》里的传递性命题)

Posted 2023-05-26

篇首语：沉舟侧畔千帆进，病树前头万木春。本文由小常识网(cha138.com)小编为大家整理，主要介绍了性质的意思(《几何原本》里的传递性命题)相关的知识，希望对你有一定的参考价值。

作者 | 刘瑞祥

所谓“传递性”是指，若a、b满足这种关系，且b、c也满足这种关系，则a和c也满足这种关系。

传递性是“等价关系”的三个要素之一，另外两个分别是：

自反性-------元素a和它自身满足这种关系；

对称性-------元素a和b若满足这种关系，则b和a也满足这种关系。

最常见、最平凡的传递性出现在相等关系中。而在《原本》的年代里，虽然还没有等价关系的概念，却有关于传递性的命题，下面简要介绍。

公理一：等于同量的量彼此相等。

这就是前面所讲的相等关系，在《原本》里，这一公理频繁地用于线段、角、面积等多个量上。下面是直接和这一公理有关的命题例子：

【l.1】在一个已知有限直线上作一个等边三角形。

这里涉及线段相等的传递性。在这一命题中，公理1的目的仅在于直接得到要证明的结论。

【l.13】一条直线和另外一条直线所交成的角，或者是两个直角或者它们的和等于两个直角。

这里涉及的是角相等的传递性。在这一命题中，公理1的作用在于将原有的两个角重新组合，进而得出结论。这可能让人觉得“非常简单”，但《原本》正是建立在这些貌似显然的命题之上的。

【l.36】在等底上且在相同二平行线之间的平行四边形彼此相等。

这是第一个涉及面积相等传递性的命题。在《原本》里如果提到两个多边形相等，根据上下文，可能是全等或者面积相等。而在【l.35】里，已经利用全等证明了同底上等高的平行四边形（面积）相等：

【l.48】如果在一个三角形中，一边上的正方形等于整个三角形另外两边上正方形的和，则夹在后两边之间的角是直角。

此即勾股定理（【l.47】）的逆定理。作者先是构造直角三角形ACD（其中AD等于AB），然后根据【l.47】得出和已知条件，由传递性得出，进而得到。接下来根据三角形全等命题边（【l.8】）得出角CAB是直角的结论。这里传递性的目的在于转化对象，为结论作准备。

【l.30】一些直线平行于同一直线，则它们也互相平行。

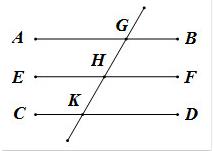
【Xl.9】两条直线平行于和它们不共面的同一直线时，这两条直线平行。

这两个命题都涉及到平行的传递性，前者是同一平面的，后者是不同平面的。在我上学的时候，教材里把这者都作为公理（其中第一条的原文是“过直线外一点能作并且只能作一条平行线”）。另外前者似乎在《原本》里很少直接应用，我只找到了一个不是太重要的：

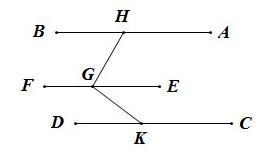
【lV.7】求作已知圆的外切正方形

书中证明了GH、FK分别和AC平行，应用【lV.7】得出GH和FK平行，类似可以得出GF和HA平行，从而证明AFGH是平行四边形，进一步可以证明该平行四边形是正方形。

虽然【lV.7】似乎不甚重要（书里只在第十二卷证明圆面积和圆锥体积的时候提到过，不过也不甚必须的），但【l.31】依然很重要，因为它能代替那条著名的而且也是很啰嗦的公设5。

【Xl.9】用来证明以下几个命题：

【Xl.10】如果相交的两条直线平行于不在同一平面内两条相交的直线，则它们的夹角相等。

【Xl.15】如果两条相交直线平行于不在同一平面上的另外两条相交直线，则两对相交直线所在的平面平行。

【Xl.38】如果一个立方体相对面的边被平分，又经过分点做平面，则这些平面的交线和立方体的对角线互相平分。

【Xl.17】已知两个同心球，在大球内作内接多面体，使它与小球面不相切。

以上的最后一个命题是为证明球体积和半径成正比做准备。这一命题是说，我们可以在大球内作一个非常贴近小球的内接多面体。

【V.11】凡与同一个比相同的比，它们也彼此相同。

比例论是《原本》的重要组成部分。在现代数学里，因为是把两个量的比看作为除法（得到一个具体的数），所以上述关于比的传递性命题无须单独论述，但《原本》里不是这样，大家可以自行查阅有关《原本》中“比例论”的介绍。这一命题运用非常频繁，至少涉及四十多个命题，下面略举数例。

这一命题首先用来比例的若干性质，如下面的更比命题：

【V.16】如果四个量成比例，则它们的更比例也成立。

原文意思是，若A:B=C:D,则A:C=B:D。这里《原本》依照比例的定义，找到一组中间量-------A、B的同倍量E和C、D的同倍量F-----作为过渡，犹如今天我们设A:B=C:D=K一样。其余如合分比、首末比的证明也类似，并且这些性质在后文的应用也非常频繁。

【Vl.2】如果一条直线平行于三角形的一边，则它截三角形的两边成比例线段……

以上即平行线等分线段命题，省略了的后半段是它的逆命题。证明方法是：如图，

【Vl.17】如果两直线被平行平面所截，则截得的线段有相同的比。

这是【Vl.2】的立体形式，直接以【Vl.2】和【V.16】作依据立刻可以得出结论。

下面还有两个传递性命题，也用到了【V.11】，不再介绍其应用。

【Vl.21】与同一直线形相似的图形，它们彼此也相似。

【X.12】与同一量可公度的两量，彼此也可公度。