怎么计算一张纸的面积(数学思想方法在小学数学中的渗透——平行四边形的面积)
Posted
篇首语:上下观古今,起伏千万途。本文由小常识网(cha138.com)小编为大家整理,主要介绍了怎么计算一张纸的面积(数学思想方法在小学数学中的渗透——平行四边形的面积)相关的知识,希望对你有一定的参考价值。
怎么计算一张纸的面积(数学思想方法在小学数学中的渗透——平行四边形的面积)
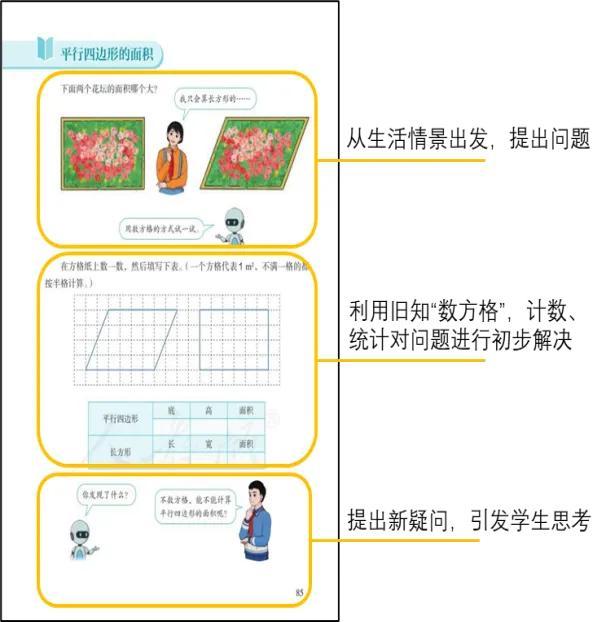
教材图选自人教版小学数学五年级上册
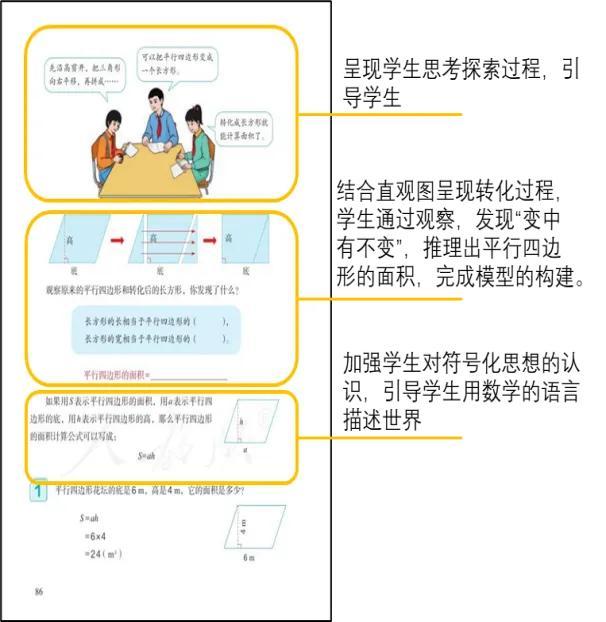
教材图选自人教版小学数学五年级上册
1.问题提出
2022年版《义务教育数学课程标准》总目标中明确提出“四基”的要求,其中基本思想依旧处于核心地位。南开大学教授顾沛提到:“数学思想的渗透,应该是长期的,一贯的。”。数学思想方法在小学课堂的渗透,有利于落实新课程理念,促进学生数学核心素养的形成。于此,笔者在阅读《吴正宪答小学数学教学50问》中‘在低年级如何渗透数学思想方法?’后,以“平行四边形的面积”教学为例浅析在课堂中如何通过操作、观察等数学活动,推导出平行四边形的面积公式,在其中渗透转化、变中有不变、类比推理、模型、数形结合等思想方法。
2.教学目标
本例选自人教版小学数学五年级上册第六单元第一课时平行四边形的面积,在本课学习前,学生已经理解平行四边形基本特征、掌握并灵活运用长方形面积计算公式。且五年级学生对空间和直观已经有了比较多的认识,生活中也积累了有关图形测量的经验。教材呈现了学生思考探索的过程,并结合直观图将平行四边形割补转化为已学过的长方形。接下来通过对图形的对比观察,发现其中的等量关系,由长方形面积公式推导出平行四边形的面积公式。于此设置以下教学目标及重难点:
教学目标:
(1)知识与技能:能运用数方格、割补法等探索并掌握平行四边形的面积计算公式,并能运用公式正确计算平行四边形面积。
(2)过程与方法:通过操作、观察、比较,发展空间观念;学会使用转化的数学思想解决实际问题。
(3)情感态度价值观:通过探究讨论活动,获得合作意识和创新精神的培养。感受数学图形的变幻及数学美,对数学产生浓厚兴趣。
教学重点:能够正确计算平行四边形的面积。
教学难点:掌握平行四边形面积计算公式的推导过程。
3.教学片段展示
3.1复习导入,提出疑问
师:这些图形大家还认识吗?
简要复习图形的边角关系等几何特征

师:那它们三个谁更大呢?
【设计意图】复习旧知,对图形的几何特征再次认识,为新知的学习做好前期准备。
3.2解决问题,探究新知
(1)数方格---长方形面积:8 正方形面积:9 平行四边形面积:8
(2)面积公式---长方形面积:长×宽 正方形面积:边长×边长
师:那平行四边形呢?它有没有面积公式呢?有的话应该是什么样子?
猜想:平行四边形面积是邻边相乘;平行四边形面积是底乘高
计算验证:错误,平行四边形不是邻边相乘算面积;正确,那是不是所有的平行四边形面积都是底乘高呢?
【设计意图】猜想有利于提高学生分析问题解决问题的能力,有利于培养学生的创造性思维。这个猜想往往是学生对于这一问题的第一解题思路,即便是不正确的,它存在的价值也不可否认,就像某一实物的发明,它一定是在多次失败中总结得到的。老师应给予鼓励,帮助建立正确的“错误观”。
(3)探索验证
师:同学们目前就只学过长方形正方形的面积公式对吧,那我们能不能用小剪刀把平行四边形剪成长方形正方形去计算面积呢?(分小组,发放卡纸剪刀,并呈现以下问题,教师观察小组活动,必要时提供帮助和指导)
问题一:转化后的长方形和之前的平行四边形有什么联系?
问题二:平行四边形面积怎么计算?
反馈交流:PPT演示剪开过程,让学生知道沿着任意高剪开都能拼凑成长方形。并提出疑问是不是所有平行四边形都能转化为面积相等的长方形,让学生空间想象拼凑的全过程。
【设计意图】学生通过裁剪对平行四边形进行转化,比较裁剪前后图形,观察分析找到中间的“不变量”,进而解决这一问题。其间涉及了转化思想、变中有不变思想,在解决问题过程中,将未知的转化为我们所熟知的内容,这常常是我们解决难题偏题的关键所在。
问题一反馈:底=长;高=宽
问题二反馈:底乘高
PPT演示平行四边形转化为长方形的过程并作公式推导(S=ah)
【设计意图】更加生动形象的呈现转化过程,所有的平行四边形都可以通过这个方法转化为长方形,进而推导出平行四边形的面积公式,构建平行四边形面积公式这一数学模型。
(4)解决问题
例题:平行四边形花坛的底是6m,高是4m,面积是多少?
3.3深入探究,拓展新知
(1)比较高不同底相同的平行四边形,体会平行四边形面积与高有关。
(2)比较高相同底不同的平行四边形,体会平行四边形面积与底有关。

(3)得出平行四边形面积与邻边无关,与底和高有关。
【设计意图】这一环节的设计加强学生对面积公式的理解,其中暗含函数思想,控制某一变量,探究因变量随自变量的变化情况,为以后函数部分的学习奠定基础。
3.4巩固应用,内化提高
(1)求以下平行四边形面积(单位:cm)


(2)一块面积为1600平方米的平行四边形花坛,如果要用篱笆把它围起来,需要多少米的篱笆?

拓展:上一题中若因为花坛翻修,所示阴影区域不需篱笆围起来,该阴影区域面积为多少平方米?(根据维果斯基最近发展区理论设计这一拓展题,为下一小节学习三角形面积公式奠定基础,学生若无法解决,教师可用PPT演示阴影区域面积为平行四边形面积的一半)
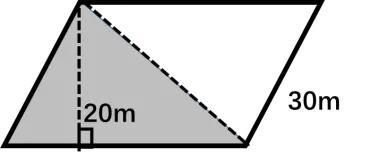
【设计意图】练习环节由易到难进行设计,后又增加拓展题,有利于学生思维的培养。该拓展题的设计有助于学生类比推理这一思想方法的形成,三角形的面积学生并未学习过,可类比平行四边形的面积的推导过程,学生自行思考尝试对这一问题进行解决。
3.5全课回顾,总结方法
对本节课内容进行回顾,总结在学习平行四边形面积过程中用到的数学思想方法。比如在面积推导过程中,学生用到了转化的数学思想方法,将平行四边形转化为长方形;掌握了平行四边形面积公式的数学模型(S=ah);在解题过程中,采用数形结合的思想方法,更好的去解决生活中的实际问题。
4.教学反思与建议
郑毓信教授曾指出:“如果您的教学始终只是停留于知识与技能的层面,您恐怕就只能算是一个‘教书匠’;如果您的教学能够很好地体现数学的思维,您就是一个‘智者’,您给学生带来了真正的智慧;然而,如果您的数学教学能给学生无形的文化熏陶,那么,即使您只是一个小学教师,即使您身处偏僻的深山或边远地区,您却是一个真正的大师,您的生命也因此而充满了真正的价值。”。我们作为小学数学教师应该在课堂中去渗透数学文化,而数学思想作为数学文化的重要组成部分,更不应该被忽略。数学思想在小学的渗透有利于提高学生发现问题、提出问题、分析问题、解决问题的能力,有利于学生数学核心素养的形成。本课例中学生通过数、剪、拼等实际操作,运用了化未知为已知的转化思想;通过猜想、验证、推理等活动完成平行四边形面积模型的构建;在剪拼过程中,沿着不同的高剪开,可以拼出同一个长方形,其中还蕴含变中有不变思想;在整个教学环节中学生始终为中心,亲身经历知识的“再发现、再创造”过程,潜移默化的进行了思想方法的渗透。思想方法不同于知识技能,不是短时间可以通过练习得来的,而是需要长时间的渗透侵染才能逐渐形成的。这就需要教师对数学思想方法有正确的认识和了解,对小学数学教材进行深入的分析和研究,在此基础上,将思想方法和教材内容进行有机融合以达到数学思想方法在小学数学课堂的渗透。
相关参考