平面图和立体图有什么区别和关系(技巧：三年级数学“画图”是帮助解题的好方法)

小学数学解题有技巧，可以根据题目内容画图，把题的条件、问题在图上标明，这样有助于我们正确审题，理解题意，从而正确解题，提高我们分析和解决问题的能力。

结合不同的内容画不同的图。通常通过平面图、立体图、分析图、线段图、表格图和思路图等，对题目的条件、问题进行展示。

下面分别举例说明。

一、平面图

对于题目中条件比较抽象、不易直接根据所学知识写出答案的问题，可以借助画平面图帮助思考解题。

例1：

有两个自然数A和B，如果把A增加12，B不变，积就增加72；如果A不变，B增加12，积就增加12O，求原来两数的积。

根据题目的条件比较抽象的特点，不妨借用长方形图，把条件转化为因数与积的关系。

先画一个长方形，长表示A，宽表示B，这个长方形的面积就是原来两数的积。

如图（1）所示：

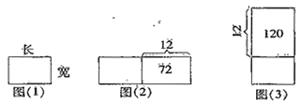
根据条件把A增加12，则长延长12，B不变即宽不变，如图（2）；

同样A不变即长不变，B增加12，则宽延长12，如图（3）。从图中不难找出：

原长方形的长（A）是120÷12＝10

原长方形的宽（B）是72÷12＝6

则两数的积为1O×6＝6O

借助长方形图，弄清了题中的条件，找到了解题的关键。

例2：

一个梯形下底是上底的1.5倍，上底延长4厘米后，这个梯形就变成一个面积为6O平方厘米的平行四边形。求原来梯形面积是多少平方厘米？

根据题意画平面图：

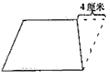
从图中可以看出：

上、下底的差是4厘米，而这4厘米对应的正好是1.5－l＝O.5倍。所以上底是4÷（1.5－1）＝8（厘米），下底是8×1.5＝12（厘米），高是6O÷12＝5（厘米），则原梯形的面积是（8＋12）×5÷2＝5O（平方厘米）。

二、立体图

一些求积题，结合题目的内容画出立体图，这样做，使题目的内容直观、形象，有利于思考解题。

例1：

把一个正方体切成两个长方体，表面积就增加了8平方米。原来正方体的表面积是多少平方米？

如果只凭想象，做起来比较困难。按照题意画图，可以帮助我们思考，找出解决问题的方法来。

按题意画立体图：

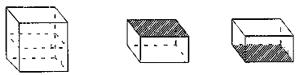
从图中不难看出，表面积增加了8平方米，实际上是增加 2个正方形的面，每个面的面积是8÷2＝4（平方米）。原正方体是6个面，即表面积为4×6＝24（平方米）。

例2：

用3个长3厘米、宽2厘米、高1厘米的长方体，拼成一个大长方体。这个大长方体的表面积是多少？

按题意画立体图来表示，三个长方体拼成的大长方体有以下三种情况：

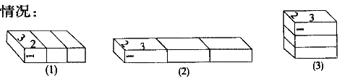
（l）拼成长方体的长是2×3＝6（厘米），宽3厘米，高1厘米。表面积为（6×3＋6×l＋3×l）×2＝54（平方厘米）。

（2）拼成长方体的长是3×3＝9（厘米），宽2厘米，高1厘米。表面积为（9×2＋9×1＋2×1）×2＝58（平方厘米）。

（3）拼成长方体的长是3厘米，宽是2厘米，高是1×3＝3（厘米）。表面积为（3×2＋3×3＋2×3）×2＝42（平方厘米）。

这道题有以上三种答案，通过画图起到审题和理解题意的作用。

三、分析图

一些应用题，为了能正确审题和分析题目中的数量关系，可以把题目中的条件、问题的相互关系用分析图表示出来。

例1：

新华中学买来 8张桌子和几把椅子，共花了 817.6元。每张桌子价 78.5元，比每把椅子贵 62.7元，买来椅子多少把？

分析图：

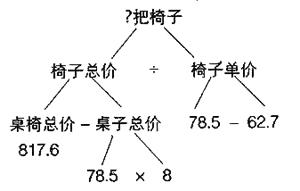
（l）买椅子共花多少钱？ 817.6－78.5×8＝189.6元）

（2）每把椅子多少钱？ 78.5－62.7＝15.8（元）

（3）买来椅子多少把？189.6÷15.8＝12（把）

综合算式为：（817.6－78.5×8）÷（78.5－62.7）

＝189.6÷15.8

＝12（把）

答：买来椅子12把。

四、线段图

一些题目条件多，条件之间关系复杂，一时难以解答。可画线段图表示，寻求解题的突破口。

例1：

光明小学六年级毕业生比全校总人数的

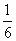
还多3O人。新学期一年级新生人学36O人，这样现在比原全校总人数增加了

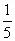
。求原来全校学生有多少人？

按照题意画线段图：

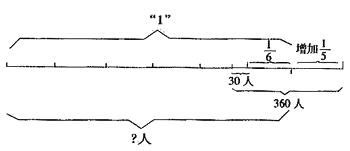
从图中可以清楚看出：

（360－30）人与全校人数的（

＋

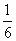
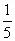
）相对应，求全校人数用除法计算。

列式为：

（360－30）÷（

＋

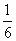
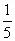
）＝330÷＝900（人）。

例2：

甲乙两人同时从相距88千米的两地相向而行，8小时后在距中点4千米处相遇。甲比乙速度快，甲、乙每小时各行多少千米？

按照题意画线段图：

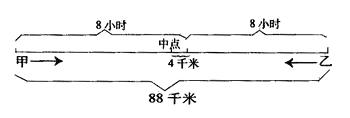
从图中可以清楚看出，甲、乙8小时各行的距离，甲行全程的一半又多出 4千米，乙行全程的一半少 4千米，这样就可以求出甲、乙的速度了。

甲速：（88÷2＋4）÷8＝6（千米）

乙速：（88÷2－4）÷8＝5（千米）

五、表格图

有些问题，通过列表不仅能分清题目的条件和问题，而且便于区分比较，起到良好的审题作用。

例1：

小明3次搬运15块砖，照这样计算，小明又搬了4次，共搬多少块砖？

根据条件、问题，列出易懂的表格，能清楚看出已知条件和所求问题。

3次

15块

又搬4次

共搬？块

从表中不难看出，又搬4次和共搬多少块，这两个数量不相对应，要先求一共搬多少次，才能求出共搬多少块，列式为：

15÷3×（3＋4）＝35（块）

另一种思路为，先求又搬4次搬的块数，再加上原有的块数，就是共搬的块数。列式为：

15÷3×4＋15＝35（块）

六、思路图

有些问题因为分析的角度不同，因此解题的思路也不同。通过画图能清楚看出解题思路，便于分析比较。

例1：

有一个伍分币、4个贰分币、8个壹分币，要拿出8分钱，一共有多少种拿法？

这道题从表面看一点也不难，但是要不重复。不遗漏地把全部拿法一一说出来也不容易，可以用枚举法把各种情况一一列举出来，把思路写出来。

五分币（1个）

1

1

贰分币（4个）

1

1

2

3

4

壹分币（8个）

1

3

6

4

2

8

拿的方法

①

②

③

④

⑤

⑥

⑦

从图表中可以清楚着出不同的拿法。此题一共有不重复的7种拿法。

从以上各例题中可看出：解题时通过画图来帮助理解题意，起到了化繁为简、化难为易的作用。我们不妨在解题中广泛使用。